The numbers $\,a,b,c\,$ is a $abc$-triplet if they are coprime and $a+b=c$. One version of the abc-conjecture is then:
For all $\varepsilon>0$ the set $E_\varepsilon$ of all $abc$-triplets with $c>\text{rad}(a\cdot b\cdot c)^{1+\varepsilon}$ is finite. where $\,\text{rad}(p_1^{n1}\cdots p_k^{n_k})=p_1\cdots p_k$ and $\,p_1,\dots ,p_k$ are arbitrary primes.
But it is known that $E_0$ is infinite. Conjecture:
For $abc$-triplets,
$(a,b,c),(a',b',c')\in E_0\,$ and $\,a^2+b^2=a'^2+b'^2\implies \{a,b\}=\{a',b'\}$
So far tested for all $a,b$ less than $10^5$. Can this be proved?
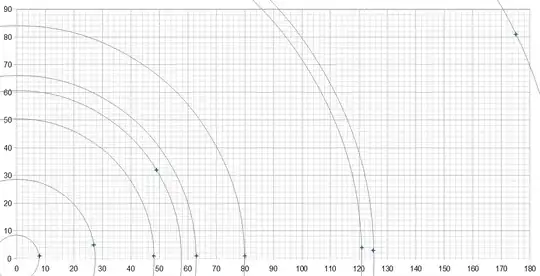
Diagram for the 9 exceptional abc-triplets with least distance to origo: $(1,8),(5,27),(1,48),(32,49),(1,63),(1,80),(4,121),(3,125),(81,175)$
http://forthmath.blogspot.se/2016/08/the-abc-conjecture-1.html