Is the Fermat primality test secure enough for very big numbers?

Question

The random variable $X_m$ is the number of trials before

$n\notin\mathbb P\wedge n\mid 2^{n-1}-1$ where $n$ is an odd random integer $2^{m-1} < n < 2^m$.

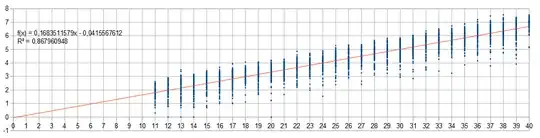
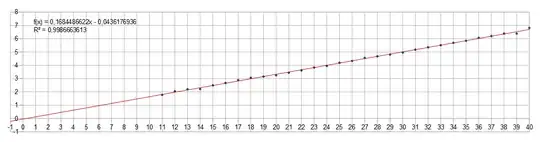
Computer simulations makes me believe that $\text E[\log X_m]=\frac{m}{6}$ and that $\operatorname{Var}[\log X_m]<1$.

I'm looking for some kind of proof of this conjecture and would like to know how to compute or estimate $P(X_{1000}=1)$, given that the conjecture is true.

The context is: how secure is the Fermat primality test with base $2$ on numbers with $1000$ binary bits? Compared with the probability of hardware errors?

Well, perhaps the 10 in the logarithm doesn't flag for an exact $\frac{m}{6}$. The regression line is $\log N= 0.1666\cdot m+0.006$ which is interpreted as $N=10^{\frac{m}{6}}$ but might also be interpreted as $N=\pi^{\frac{m}{3}}$ within the marginals. $\overset{..}{\smile}$

$3251$ simulations total so far. Some lower experiments $(m=10)$ has been removed, since lower intervalls gives more irregular results. In some intervalls there are no discrepancies. Also long time running results from $m=40$ is included, so the equation of the line of regression has changed a little.

Diagram of the mean values of each m

So you want the number of $m$-bit base-2 Fermat Pseudooprimes, and your simulations hint to these making up approximately a share of $2^{6/m}$ of all odd $m$-bit numbers? — Hagen von Eitzen, Jun 21 '16 at 09:39
@HagenvonEitzen, as I see it, it would be $1$ chance of $10^{m/6}$ to find such an odd number in the intervall $[2^{m-1},2^{m})$. — Lehs, Jun 21 '16 at 12:19

score 5 · Answer 1 · edited Apr 13 '17 at 12:20

Note that this Question deals with base 2 Fermat pseudoprimes rather than strong pseudoprimes as mentioned in one of the OP's earlier Questions.

Carl Pomerance ("On the Distribution of Pseudoprimes", 1981) bounds the count $P_2(x)$ of base 2 Fermat pseudoprimes less than $x$:

$$ \exp\left\{ (\log x)^{5/14} \right\} \le P_2(x) \le x \cdot L(x)^{-1/2} $$

where $$L(x) = \exp\left( \frac{(\log x) (\log \log \log x)}{\log \log x} \right) $$

Pomerance conjectures that $P_2(x) = x \cdot L(x)^{-1 + o(1)}$.

A nice exposition for these results is given by Matt Green ("The Distribution of Pseudoprimes", 2002).

The present Question asks about the probability that an odd number $X_{1000}$ chosen uniformly from:

$$ 2^{999} \lt X_{1000} \lt 2^{1000} $$

will be one of these base $2$ Fermat pseudoprimes (also known as Poulet numbers or even more obscurely, Sarrus numbers).

Now $L(2^{1000}) \approx exp\left(199.0170124\right) $ can be computed, and a corresponding upper bound and estimate of this probability will follow.

@Lehs: Right, I'll add some parentheses. These iterated logs come up so often that number theorists have a special notation, $\log_k x$ for the $k$-times composition of the natural logarithm. — hardmath, Jun 21 '16 at 18:11

score 1 · Answer 2 · answered Apr 05 '17 at 17:36

An interesting variant brings a very high probability that a given number is prime (See here : https://primes.utm.edu/notes/prp_prob.html )

Suppose, you have a random number $n$ and you choose a random base $1<a<n$. If $a^{n-1}\equiv 1 \mod n$, then $n$ is very probable prime. The table in the link gives upper bounds. Even ONE WEAK Fermat-test is completely sufficient in the case of $1000$ or more bits.

If you still have doubts you can also apply the strong-probable-prime-test. And for numbers with several hundred digits the Adleman-Pomerance-Rumely-test proves the primality and is still surprisingly fast.

PARI/GP for example supports this routine and an example with $300$ digits took me $16$ seconds to prove the primality.

Is the Fermat primality test secure enough for very big numbers?

2 Answers2