0

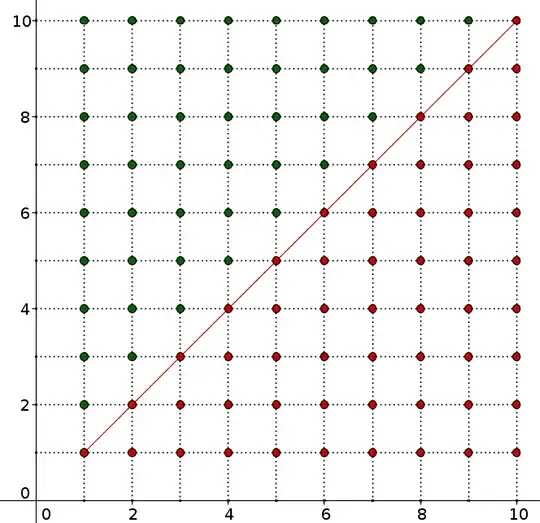
This is an extension to the question.

Given two randomly chosen natural numbers from 1 to 10, what is the probability that the second is greater than the first?

For first number to be $1$ and second number to be $2-10$, probability is $\dfrac{1}{10}×\dfrac{9}{10}$

So are the other cases.

so, probability that the second is greater than the first

$=\dfrac{1}{10}×\dfrac{9}{10}+\dfrac{1}{10}×\dfrac{8}{10}+\cdots+\dfrac{1}{10}×\dfrac{1}{10}=\dfrac{45}{100}$

So, I am getting $\dfrac{45}{100}$ as the answer.

When things goes to infinity, this will become close to $\dfrac{1}{2}$

Why my answer and approach leading to wrong answer then?

Community
  • 1
Kiran
  • 4,353
  • 1
    Numbers are chosen with or without replacement? – Qwerty Jun 16 '16 at 13:22
  • 5
    Probability of a tie is $\frac {10}{100}$. Absent a tie, there are equal chances for first or second to be greater. Hence $\frac 12 \times \left(1-\frac {10}{100}\right)=\frac {45}{100}$. What's the problem? As the ceiling goes to $\infty$ the probability of a tie goes to $0$. – lulu Jun 16 '16 at 13:22
  • @Qwerty, with replacement – Kiran Jun 16 '16 at 13:33

3 Answers3

4

There is a pretty convincing geometric argument for the probability to be $\frac{1}{2}-\frac{1}{20}=\color{green}{\large 45\%}$:

enter image description here

In the general case, it is $\frac{1}{2}-\frac{1}{2n}\to\frac{1}{2}$. The number of integer points on a diagonal of a square is negligible with respect to the number of integer points inside the whole square (the first number is approximately the square root of the latter).

Jack D'Aurizio
  • 361,689
3

For the integers $1$ to $n$, the probability that the second is greater than the first is, by extension of your argument, $$\frac{n-1}{2n}$$ which tends to $\frac 12$ as $n\rightarrow\infty$

David Quinn
  • 35,087
1

$\displaystyle{\sum_{n = 1}^{10}{1 \over 10}\left(10 - n\right)\,{1 \over 10} ={1 \over 10}\times 10 - {1 \over 100}\,{10\times 11 \over 2} = 1 - 0.55 = \color{#f00}{0.45}}$

Felix Marin
  • 94,079