Is this comb-like space contractible?

Question

For each $ \ n \in \mathbb{N}^* = \{ 1,2,3,4,... \}$, let $ \ S_n = \big\{ (t,1-nt) \in \mathbb{R}^2 : 0 \leqslant t \leqslant 1/n \big\}$, $Y_n = \big\{ (t,-nt-1) \in \mathbb{R}^2 : -1/n \leqslant t \leqslant 0 \big\}$, $\displaystyle S = \bigcup_{n \in \mathbb{N}^*} S_n$, $\displaystyle Y = \bigcup_{n \in \mathbb{N}^*} Y_n \ $ and $ \ Z = \{ 0 \} \times [-1,1]$. Consider $ \ X = Y \cup Z \cup S$, with the subspace topology inherited from the euclidean usual topology of $ \, \mathbb{R}^2$. I have attached a picture of the space below.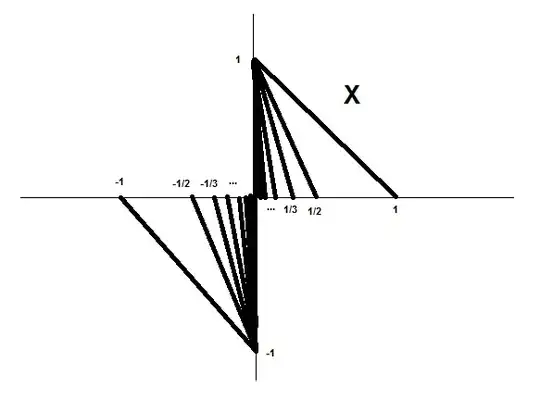

My questions are

$(1) \ $ Is this space $X$ contractible? Why? How can I prove it?

$(2) \ $ How can I compute the homotopy groups of $X$?

I think the answer for $(1)$ is no. I have tried to prove it by contradiction. Suppose it is. So, we have homotopy equivalences $ \ f : X \to * \ $ and $ \ g: * \to X \ $ such that $ \ f \circ g \sim id_* \ $ and $ \ g \circ f \sim id_X \, $. Then, there exists a homotopy $ \ H: X \times I \to X \ $ such that $ \ H(x,0) = x \ $ and $ \ H(x,1) = g \big( f(x) \big),$ $\forall x \in X$. I think this will let me to some contradiction, but I am stuck.

For $(2)$ it is even worse. I have tried to visualize the image of some general continuous map $ \ f : S^n \to X \ $ in $X$, but I see nothing.

Any help will be highly appreciable.

Answer 1

As for the second question:

Claim: Any continuous map $f:S^n\to X$ can be homotoped to a map whose image is contained in $S\cup Z$.

Given $f:S^n\to X$, define a homotopy

$$\begin{array} &H:S^n\times I\to X&\\ (x,t)\mapsto\begin{cases} f(x) &\mbox{if } f(x)\in S\cup Z \\ tf(x)+(1-t)(0,-1) & \mbox{if } f(x)\in Y \end{cases} \end{array}$$ $H$ is well-defined, continuous, $H_1=f$ and the image of $H_0$ lies in $S\cup Z$.

This proves that $\pi_n(X)=0$ since $S\cup Z$ is contractible (it deformation retracts onto $(0,1)$).