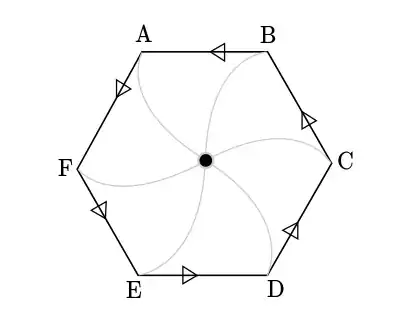
Suppose we have a regular polygon with $n$ sides. On each vertex, there is a particle. Every particle moves in such a way that its velocity vector $(\vec{v})$ always points towards particle next to it. The velocity vectors of all particles are equal in magnitude.
How do we show that the meet at centroid of the polygon.
Actually, the problem was in physics, and it asked the time particle took to reach the centroid. The time can easily be calculated using resolution of components of vectors.