Prove that $(x+y+z)^2(yz+zx+xy)^2 \leq 3(y^2+yz+z^2)(z^2+zx+x^2)(x^2+xy+y^2)$

Question

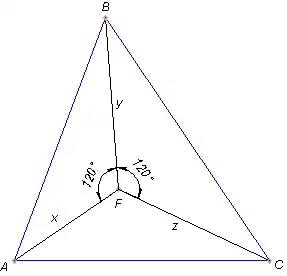
This is Problem 6 of the 2007 Indian National Math Olympiad (INMO).

If $x, y, z$ are positive real numbers, prove that $(x+y+z)^2(yz+zx+xy)^2 \leq 3(y^2+yz+z^2)(z^2+zx+x^2)(x^2+xy+y^2).$

My best idea was to expand this and simplify. Although that doesn't look very feasible. Another idea is to see that $x^2+y^2+xy \geq x^2+y^2$. Then we just have to show that $(x+y+z)^2(yz+zx+xy)^2 \leq 3(x^2+y^2)(x^2+z^2)(y^2+z^2)$ if that is even true.

This might not be desirable, but I think you could probably prove it by simply expanding out all the terms and canceling things. There is probably a much faster way. — nukeguy, Feb 19 '16 at 19:14
I see that you have upvoted only 13 times for answers and you have 102 posted questions with even more answers ... — Svetoslav, Feb 19 '16 at 19:26
Don't you see the strange signs in the inequality and in the title ? You have copied it from somewhere and even didn't delete them. — Svetoslav, Feb 19 '16 at 19:27
@Svetoslav I actually didn't copy them and I put everything in latex form. — Puzzled417, Feb 19 '16 at 19:29
The pqr method which is not nice: Let $p = x+y+z, q = xy+yz+zx, r=xyz$. We have $\mathrm{RHS} - \mathrm{LHS} = -3p^3r+2p^2q^2-3q^3$. Since $q^2 \ge 3pr$, it suffices to prove that $-3p^3\frac{q^2}{3p}+2p^2q^2-3q^3\ge 0$ or $q^2(p^2-3q) \ge 0$ which is true since $p^2 \ge 3q$. — River Li, Sep 02 '20 at 13:58

score 2 · Answer 1 · answered Jan 05 '18 at 13:04

2

Let $AF=x\ , BF=y\ , CF=z$.

$F-$ Fermat point of $\triangle ABC\ $

So inequality we can rewrite as : $x+y+z\le 3R$ , which is obviously true)

answered Jan 05 '18 at 13:04

Sergic Primazon

708

score 1 · Answer 2 · answered Feb 21 '16 at 00:42

1

$(x+y+z)^2=x^2+y^2+z^2+2xy+2yz+2xz \\ \le x^2+xy+y^2+y^2+yz+z^2+x^2+xz+z^2$

$3(y^2+yz+z^2)(z^2+zx+x^2)(x^2+xy+y^2)-(x^2+xy+y^2+y^2+yz+z^2+x^2+xz+z^2)(yz+zx+xy)^2=(x+y+z)^2(y^2z^2-xyz^2+x^2z^2-xy^2z-x^2yz+x^2y^2) \ge0$

answered Feb 21 '16 at 00:42

chenbai

7,681

score 1 · Answer 3 · edited Feb 22 '25 at 10:50

1

Let $I = 3(x^2 + xy + y^2)(y^2 + yz + z^2)(z^2 + zx + x^2)$. Then, by Hölder's Inequality, it follows that: $$I ≥ 81x^2y^2z^2$$ Thus, we need to prove that: $$81x^2y^2z^2 ≥ (x + y + z)^2(xy + yz + zx)^2 \Longrightarrow 9xyz ≥ (x + y + z)(xy + yz + zx)$$

Expanding the RHS gives: $$9xyz ≥ xy(x + y) + yz(y + z) + zx(z + x) + 3xyz$$ $$xy(x + y) + yz(y + z) + zx(z + x) ≥ 6xyz$$ which is evidently true by the AM-GM inequality.
Q.E.D. $\blacksquare$

edited Feb 22 '25 at 10:50

Joyneel Bepari

1,342

answered Nov 21 '22 at 15:51

Karan Gupta

19

Welcome to MSE! Please format answers using MathJax for readability. – Moo Nov 21 '22 at 16:18
The last bit of this response isn't true! – Joyneel Bepari Feb 22 '25 at 10:26

Michael Rozenberg · Answer 4 · 2016-02-19T20:23:27.497

0

We'll prove that our inequality is true for all reals $x$, $y$ and $z$.

Indeed, let $x+y+z=3u$, $xy+xz+yz=3v^2$ and $xyz=w^3$.

Since $\prod\limits_{cyc}(x^2+xy+y^2)=27(3u^2v^4-u^3w^3-v^6)$,

we see that our inequality is equivalent to $f(w^3)\geq0$, where $f$ is a linear function.

Thus, $f$ get's a minimal value for an extremal value of $w^3$.

Since $x$, $y$ and $z$ are real roots of the equation $(X-x)(X-y)(X-z)=0$ or

$X^3-3uX^2+3v^2X-w^3=0$ or $X^3-3uX^2+3v^2X=w^3$, we see that a line $Y=w^3$ and a graph $Y=X^3-3uX^2+3v^2X$ should have three common points and the extremal value of $w^3$ happens for the equality case of two variables.

Since our inequality is homogeneous and even degree, it remains to check one case only: $y=z=1$,

which gives $(x-1)^2(5x^2+8x+5)\geq0$. Done!

edited Feb 19 '16 at 20:23

answered Feb 19 '16 at 19:35

Michael Rozenberg

203,855

Why are $x,y,z$ roots of $(X-x)(X-y)(X-z) = 0$? – Puzzled417 Feb 19 '16 at 19:52
@ Puzzled417 $x$ a root of $(X-x)(X-y)(X-z)=0$ because $(x-x)(x-y)(x-z)=0$ is true. – Michael Rozenberg Feb 19 '16 at 19:57
Why does the extremal value of $w^3$ happen for the equality case of two variables? – Puzzled417 Feb 19 '16 at 20:06
Also how did you decide to use $3u,3v^2,w^3$? – Puzzled417 Feb 19 '16 at 20:09
Draw a graph of $Y=w^3$ (it's a line paralleled to OX) and a graph of $Y=X^3-3uX^2+3v^2X$ and change $w^3$ such that two graphs have three common points. I am sure that you'll see it! – Michael Rozenberg Feb 19 '16 at 20:13
What is $OX$ I don't get? – Puzzled417 Feb 19 '16 at 20:16
@Puzzled417 OX it's X axis – Michael Rozenberg Feb 19 '16 at 20:19
Do you mean $xyz = w^3$? – Puzzled417 Feb 19 '16 at 20:22

score 0 · Answer 5 · answered Feb 22 '25 at 10:17

By simple rearrangement, one can assert that: $$4\left(x^2 + xy + y^2\right) ≥ 3(x + y)^2 \Longrightarrow x^2 + xy + y^2 ≥ \dfrac{3(x + y)^2}{4}$$ Applying this cyclically gives: $$3\prod_\text{cyc}\left(x^2 + xy + y^2\right) ≥ \dfrac{81}{64}\prod_\text{cyc}(x + y)^2$$ Now, it is left to show that: $$\dfrac{81}{64}\prod_\text{cyc}(x + y)^2 ≥ (x + y + z)^2(xy + yz + zx)^2$$ which is the same as showing that: $$9(x + y)(y + z)(z + x) ≥ 8(x + y + z)(xy + yz + zx)$$ A useful identity states that: $$(x + y + z)(xy + yz + zx) = (x + y)(y + z)(z + x) + xyz$$ and so, we are ideally meant to prove that: $$(x + y)(y + z)(z + x) ≥ 8xyz$$ which is indeed true by the AM-GM inequality applied cyclically thrice to $x + y$, $y + z$, and $z + x$.

Therefore: $$\boxed{3\prod_\text{cyc}\left(x^2 + xy + y^2\right) ≥ (x + y + z)(xy + yz + zx)}$$ Q.E.D. $\blacksquare$

Prove that $(x+y+z)^2(yz+zx+xy)^2 \leq 3(y^2+yz+z^2)(z^2+zx+x^2)(x^2+xy+y^2)$

5 Answers5

Linked

Related