0

I'm trying to find an interpolating formula for a set of coefficients (I have $80$ at the moment).

I tried first to find an interpolating polynomial, but that was not useful: using the first $40$ coefficients only and extrapolate that formula to a guess for the other $40$ coefficients leads to catastrophic error.

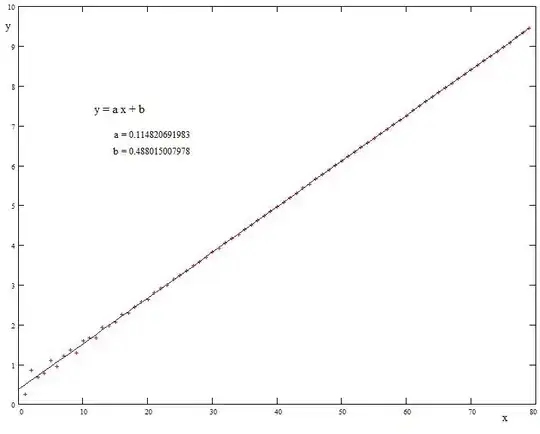
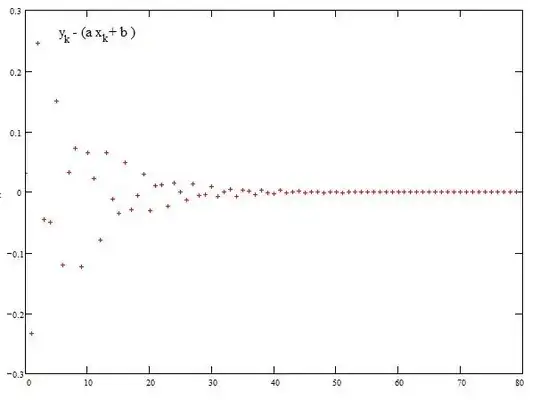
So I tried another path: first find a linear expression which interpolates as smooth as possible (simple linear regression). Then it seems, that the reciprocals of the residuals might be best approximated by a next step of linear regression - and after some manual guesses it seems, that it is again most appropriate to use again the reciprocals of the new residuals with a linear or a quadratic curve - and possibly so on.

The idea for a regression formula were thus the following with $2$ pairs of parameters where the coefficients are indicated by $y_k$ ,$N=40$ and $k=1..N$ : $$ \sum_{k=1}^N \left( {1 \over y_k -(a_0+a_1 k) } - (b_0+b_1 k) \right)^2 \overset{!}{=} min $$

Possibly this must then be continued by a next step, where again the reciprocals of the new residuals must be approximated by a quadratic regression, so in principle I look for some algorithm which will be mechanically extensible, but that's only the next step. So just for a start:

Q: What would be the formula to determine the four parameters?

See the requested data in a separate "answer" to keep the question better readable.

[update] P.s. : I've had similar problems casually in earlier problems (from my numbertheory fiddlings), and got in such cases stuck with some manual optimizations - so the principle of such a regression would serve me enough, please don't put too much effort in some extreme finetuning of the parameters on base of that 80 datapoints.

[update2] A bit more background to avoid misconceptions and to avoid frustration to someone willing to help. The data stem from a problem in number theory (see here in MSE) where I found a sequence of (infinitely many) points which seem to approximate to a linear or near linear decrease (linear with the index).
The problem is the following. Begin with the complex number $z_0=1$. Iterate $z_{k+1}=î ^ z_k$ (where $î$ is the imaginary unit) which process converges to a fixpoint $t$. Take the (euclidean) distance $d$ of each iterate $d_k = |z_k - t|$ . The given data $y_k$ are the $\log()$ of the $d_k$.

There is very likely no simpler function for that values available, but a functional approximation to the $y_k$ seems to be primarily linear with some unknown, diminuishing secondary distortion, again systematic.
A good approximation is enough for my purposes, but must be robust for extrapolation to infinitely many datapoints. I need not only one "practical" approximation but a method because the same problem with improving approximation to linearity occurs as well with the angular value $ \arg(z_k-t)$ for which I want then apply the same procedure.
Trying to find a working model using the ansatz of regression brought me to the above formula with four parameters (for a start) which I cannot expand/resolve for a formal solution.

Community
  • 1
Gottfried Helms
  • 35,815
  • Can we see your data ? –  Feb 05 '16 at 08:42
  • @Yves : I've put the data into an answer-box to not to clutter the question too much. – Gottfried Helms Feb 05 '16 at 09:09
  • Not sure what you are trying to do. After initial oscillations, the fit to a line gets better and better as the point index increases. Why do you split in two subsets ? –  Feb 05 '16 at 09:50
  • @Yves: the splitting is done to have some sanity check of the procedure. For how many current data-points I'll do any optimizaton, there will be infinitely many more for which that optimization must be sensical. The problem is that an estimation will always face the problem that I have to extrapolate to hiher indexes. So this splitting shall give some indication, whether the found optimization can be meaningful at all. Consider the polynomial interpolation. I did it with first forty points and got exact fit. But extrapolated to further points showed catastrophic error, so this splitting... – Gottfried Helms Feb 05 '16 at 10:29
  • ... was an instrument to uncover the inappropriateness of the polynomial interpolation at all. I think the same applies to any method - even with this regression-model. – Gottfried Helms Feb 05 '16 at 10:30
  • Polynomial interpolation is indeed unusable above, say, ten points. But regression behaves very well, except in the case of outliers. In your case I see a nice linear law and I wonder why you want to complexify the model. The initial points are a little dangerous because of the oscillations, which aren't modelled, but they decay steadily. I would just ignore the first 20 or so. I still can't understand your intent. –  Feb 05 '16 at 10:40
  • @Yves - well actually I used that linear interpolation as rough approximation (as well as a more sophisticated formula, but that's complete different path, see the new link in my updated answer). I just saw room for improvement and tried to make sense of the above regression-model. My problem is simply to derive the solution for the parameters for a regression, where the data-to-be-fit (resp. the intended residuals) are in the denominator of the regression-formula which is quite unusual for me. I thought there might be some (simple) canonical answer for such a question. – Gottfried Helms Feb 05 '16 at 11:11
  • From what I have seen, the residuals are oscillating around a straight line and adding non-oscillating terms won't help. But I can be wrong. –  Feb 05 '16 at 11:26

3 Answers3

1

Based on your initial question and using the values you give, I considered the function $$F(a_0,a_1,b_0,b_1)=\sum_{k=1}^{80} \left( {1 \over y_k -(a_0+a_1 k) } - (b_0+b_1 k) \right)^2 $$ and I just minimized it numerically.

The minimum is found for the following parameters $$a_0=36.9437\quad a_1=-0.127637$$ $$b_0=-0.0268729\quad b_1=-9.57943 \times 10^{-6}$$ for which $F_{opt}=1.06724\times 10^{-7}$

Claude Leibovici
  • 289,558
  • Hi Claude! Very nice - I had given up because of an insufficient test-environment for simultanously adapt four parameters... I'll see what this gives to me, thanks so far! – Gottfried Helms Feb 06 '16 at 13:17
0

Data which I'm working on. I use $80$ values but put it here in two portions a $40$ (vertically). I'm getting an approximation-formula from the left block of forty values and check the appropriateness by application to the full dataset. The left column of each block is the index which begins at $1$ to allow formulae with reciprocals. The data stem from a formula by which I can successively get infinitely more values (but practically limited to some $100$ or $200$ data-points)

  1. data in csv-format: file
  1. data in mathjax-format:

$$\small \begin{array} {rl|rl} 1 & -0.404219547134 & 41 & -4.96369610919 \\ 2 & -0.254635150576 & 42 & -5.08346228643 \\ 3 & -0.848826900252 & 43 & -5.19387328015 \\ 4 & -0.672497295471 & 44 & -5.30980799271 \\ 5 & -0.782648581294 & 45 & -5.42691064949 \\ 6 & -1.09661390701 & 46 & -5.53829673204 \\ 7 & -0.941305565047 & 47 & -5.65523782695 \\ 8 & -1.20932963584 & 48 & -5.77042934573 \\ 9 & -1.36432295221 & 49 & -5.88318317015 \\ 10 & -1.28358177556 & 50 & -6.00009058654 \\ 11 & -1.58603096933 & 51 & -6.11423257056 \\ 12 & -1.65776438414 & 52 & -6.22820436618 \\ 13 & -1.67153909479 & 53 & -6.34456590114 \\ 14 & -1.93014001210 & 54 & -6.45835690750 \\ 15 & -1.96844248450 & 55 & -6.57316075367 \\ 16 & -2.06003832171 & 56 & -6.68885932414 \\ 17 & -2.25865650761 & 57 & -6.80273947156 \\ 18 & -2.29610558688 & 58 & -6.91796901573 \\ 19 & -2.43438066384 & 59 & -7.03311492793 \\ 20 & -2.58368257882 & 60 & -7.14728282076 \\ 21 & -2.63902124916 & 61 & -7.26262536683 \\ 22 & -2.79434601545 & 62 & -7.37741464273 \\ 23 & -2.91134973187 & 63 & -7.49189688720 \\ 24 & -2.99089127097 & 64 & -7.60716668365 \\ 25 & -3.14368853097 & 65 & -7.72178845853 \\ 26 & -3.24410305971 & 66 & -7.83651835597 \\ 27 & -3.34517482343 & 67 & -7.95164075044 \\ 28 & -3.48674797680 & 68 & -8.06623261683 \\ 29 & -3.58231400466 & 69 & -8.18111355575 \\ 30 & -3.69791558146 & 70 & -8.29608865051 \\ 31 & -3.82709089874 & 71 & -8.41072732188 \\ 32 & -3.92498019330 & 72 & -8.52567229447 \\ 33 & -4.04770179897 & 73 & -8.64053766338 \\ 34 & -4.16709403679 & 74 & -8.75524974887 \\ 35 & -4.27042930487 & 75 & -8.87019875417 \\ 36 & -4.39467132300 & 76 & -8.98500120459 \\ 37 & -4.50802943507 & 77 & -9.09978136831 \\ 38 & -4.61704538184 & 78 & -9.21470325795 \\ 39 & -4.73962423078 & 79 & -9.32948231359 \\ 40 & -4.85032671658 & 80 & -9.44431053345 \end{array}$$

  1. data in textformat:

data 

   1  -0.404219547134  41  -4.96369610919
   2  -0.254635150576  42  -5.08346228643
   3  -0.848826900252  43  -5.19387328015
   4  -0.672497295471  44  -5.30980799271
   5  -0.782648581294  45  -5.42691064949
   6   -1.09661390701  46  -5.53829673204
   7  -0.941305565047  47  -5.65523782695
   8   -1.20932963584  48  -5.77042934573
   9   -1.36432295221  49  -5.88318317015
  10   -1.28358177556  50  -6.00009058654
  11   -1.58603096933  51  -6.11423257056
  12   -1.65776438414  52  -6.22820436618
  13   -1.67153909479  53  -6.34456590114
  14   -1.93014001210  54  -6.45835690750
  15   -1.96844248450  55  -6.57316075367
  16   -2.06003832171  56  -6.68885932414
  17   -2.25865650761  57  -6.80273947156
  18   -2.29610558688  58  -6.91796901573
  19   -2.43438066384  59  -7.03311492793
  20   -2.58368257882  60  -7.14728282076
  21   -2.63902124916  61  -7.26262536683
  22   -2.79434601545  62  -7.37741464273
  23   -2.91134973187  63  -7.49189688720
  24   -2.99089127097  64  -7.60716668365
  25   -3.14368853097  65  -7.72178845853
  26   -3.24410305971  66  -7.83651835597
  27   -3.34517482343  67  -7.95164075044
  28   -3.48674797680  68  -8.06623261683
  29   -3.58231400466  69  -8.18111355575
  30   -3.69791558146  70  -8.29608865051
  31   -3.82709089874  71  -8.41072732188
  32   -3.92498019330  72  -8.52567229447
  33   -4.04770179897  73  -8.64053766338
  34   -4.16709403679  74  -8.75524974887
  35   -4.27042930487  75  -8.87019875417
  36   -4.39467132300  76  -8.98500120459
  37   -4.50802943507  77  -9.09978136831
  38   -4.61704538184  78  -9.21470325795
  39   -4.73962423078  79  -9.32948231359
  40   -4.85032671658  80  -9.44431053345
Gottfried Helms
  • 35,815
0

If I well understand the question, you have the data $(x_k\:,\:y_k)$ where $k=1$ to $k=n$ ( in your example $n=80$ and $x_k=k$ ).

As the problem is settled, this is not exactly the fitting of a function to the data but in fact the fitting of an equation to the data, which is slightly different. The equation is : $$\frac{1}{y-(a_0+a_1x)} - (b_0+b_1x)=0$$ The goal is to find approximates for $a_0\:,\:a_1\:,\:b_0\:,\:b_1$ so that the equation be at best satisfied. $$ \left(y-(a_0+a_1x)\right)(b_0+b_1x)-1=0$$ $$b_0y+b_1xy-(a_1b_0+a_0b_1)x-a_1b_1x^2=1+a_0b_0$$ Let : $\quad C_1=\frac{b_0}{1+a_0b_0}\quad;\quad C_2=\frac{b_1}{1+a_0b_0}\quad;\quad C_3=-\frac{a_1b_0+a_0b_1}{1+a_0b_0}\quad;\quad C_4=-\frac{a_1b_1}{1+a_0b_0}$

Then, compute for $k=1$ to $k=n$ : $\quad p_k=x_ky_k \quad \text{and}\quad q_k=x_k^2$

The regression with linear mean square fitting of : $$C_1y_k+C_2p_k+C_3x_k+C_4q_k\simeq1$$ will lead to $\:C_1\:,\:\:C_2\:,\:\:C_3\:,\:\:C_4\:$. Then, with the four relationships with $\:a_0\:,\:\:a_1\:,\:\:b_0\:,\:\:b_1\:$ one can compute the approximates of those four parameters.

enter image description here

I didn't test this method with your data because a simple linear regression seems convenient and leads to a very good fitting , or have I missed something ? :

enter image description here

enter image description here

JJacquelin
  • 68,401
  • 4
  • 40
  • 91
  • Hmm, the rationale of the "regression" is the minimization of the error of prognosis in the sense of the least (sum-of) squares of the residuals. Now I'm missing the "squares" and the "sum" and the "minimum" in your first equation where you equal the lhs to zero. Speaking of "minimization" the derivative of a function should become zero (and the second derivative should become positive), not the function itself. Did I misread something in your ansatz? – Gottfried Helms Feb 05 '16 at 10:36
  • Thre is no derivative at all in this method. As I said, it is not the usual mean square fitting in the sense of fitting a curve to data : http://mathworld.wolfram.com/LeastSquaresFitting.html . It is the fitting of an equation (wich is in fact the inplicit expression of the equation of the curve) : Section 5, page 10 in : https://fr.scribd.com/doc/14819165/Regressions-coniques-quadriques-circulaire-spherique . – JJacquelin Feb 05 '16 at 10:49
  • To clearify this point, see the addidion to my first answer. But, of course, if it is strictly required the least squares with the common definition of the residuals, you have to use a non-linear method , for example : http://mathworld.wolfram.com/NonlinearLeastSquaresFitting.html – JJacquelin Feb 05 '16 at 11:06
  • I added a link to a *.csv-file in my answer which contains the sample of data – Gottfried Helms Feb 05 '16 at 11:29
  • I think now, that a simple answer is not possible since it is a non-linear regression-problem and I've to finetune any final approximation manually. So I just want to say thank you very much for all your help! – Gottfried Helms Feb 05 '16 at 11:54
  • With the new link I got the sample of data. See the addition to my previous answer. – JJacquelin Feb 05 '16 at 13:39
  • Step 1: Yes, I've done the same regression and got the same/a similar result. Step 2: But after that I looked at the residuals and noticed, that they have a trend to become absolutely smaller. So I considered to do a further improvement to find a characteristic of that. Looked at the residuals and at their reciprocals - observing/guessing that there is another linear trend. Thus the residuals of Step 1(as of your finding) are in the denominator of my formula and I tried -as a higher order approximation- to get something useful by removing that trend. That's the reason for my complete formula. – Gottfried Helms Feb 05 '16 at 14:32
  • OK. But looking at the magnitude of scatter on the left side of the curve, on my pinion, such an expected improuvement is questionable . Anyways, you are the sole judge. – JJacquelin Feb 05 '16 at 14:45