Possible all-Pentagon Polyhedra

Question

If a polyhedron is made only of pentagons and hexagons, how many pentagons can it contain? With the assumption of three polygons per vertex, one can prove there are 12 pentagons.

Let's not make that assumption, and only use pentagons.

12 pentagons: dodecahedron and tetartoid.
24 pentagons: pentagonal icositetrahedron.
60 pentagons: pentagonal hexecontahedron.
72 pentagons: dual snub truncated octahedron.
132 pentagons: 132-pentagon polyhedron.
180 pentagons: dual snub truncated icosahedron.

Here's what the 132 looks like.

In that range of 12 to 180, what values are missing? For values missing here where an all-pentagon polyhedron exists, what is the most symmetrical polyhedron for that value?

Edit: According to Hasheminezhad, McKay, and Reeves, there are planar graphs that lead to 16, 18, 20, and 22 pentagonal faces, but I've never seen these polyhedra.

16 would be the dual of the snub square antiprism.
20 would be the dual of this graph:

Can't you partition each pentagon into six pentagons (like with the six pentagons in the center of your image), making it potentially infinite? — Akiva Weinberger, Jan 12 '16 at 21:10
That would technically make the surrounding pentagons into hexagons. — Ed Pegg, Jan 12 '16 at 22:00
@akiva use an $11$-way division with two rings around the central pentagon. Now the adjacent faces are undisturbed. — Oscar Lanzi, Jan 17 '17 at 02:32
So removing a face from the dodecahedron, projecting the remaining figure onto the plane to get a pentagon made of 11 pentagons (and unbroken edges), and using that to replace a pentagon of a given pentagonal solid)? @OscarLanzi — Akiva Weinberger, Jan 17 '17 at 02:49
@OscarLanzi Which is topologically equivalent to your answer. I see. — Akiva Weinberger, Jan 17 '17 at 16:35

score 5 · Answer 1 · answered Jan 16 '16 at 22:45

You can get $4k$ pentagonal faces for any $k≥3$. Take $k$ pentagons meeting at a point (in the plane, or on a sphere). Between each adjacent pair of pentagons, draw another pentagon, making a second ring of $k$ pentagons. Each of the original $k$ pentagons has a single exposed edge left; to this edge and the adjacent two edges of second-ring pentagons, add two more to form a new pentagon. This makes a third ring of $k$ pentagons. Joining the $k$ new vertices of this ring to a single point completes a fourth ring of $k$ pentagons.

graph with k=5

Having drawn the planar graph, Steinitz's theorem says such a polyhedron exists.

The initial vertex, and the final vertex, have degree $k$; all other vertices have degree three. When $k=3$ this is a standard construction of the regular dodecahedron.

The polyhedron can be made with an axis of $k$-fold rotation through the two vertices of degree $k$; we also have reflections and a half-turn taking one such vertex to the other, for at least $4k$ symmetries.

On the other hand, clearly the number of faces must be even (since 5 times the number of faces is twice the number of edges). So, the remaining possibilities for the number of faces are equivalent to 2 mod 4.

You can also start with one pentagon, attach an even number $\ge 2$ of five-pentagon rings, and close with a single pentagon. This gives $10n+2$ faces, comparable to my own answer. — Oscar Lanzi, Jan 17 '17 at 01:23
What you describe here is just the dual of the snub k-gonal antiprism. The snub trigonal antiprism is the icosahedron, thus its dual is the dodecahedron, as you said. The 4-gonal and 5-gonal faces have already been given by the questioner. — Dr. Richard Klitzing, Oct 07 '24 at 12:28

Oscar Lanzi · Accepted Answer · 2025-06-03T20:35:28.810

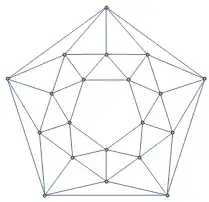
There is an easy way to get a polyhedron with $10n+2$ pentagons only.

Start with a regular dodecahedron. Take a congruent dodecahedron and merge it face to face with the first one, removing the merged faces to get an increment of $10$ faces. Repeat as desired with additional regular dodecahedra.

Yes, it's ugly, in that we lack convexity and don't have elegant symmetry (for $n \ge 2$). But it systematically makes infinitely many numbers of faces work, and the faces themselves are regular.

Addendum:

Following up on @Kundor's answer, we can interpret this in terms of graph theory. When we merge an additional dodecahedron into the figure, we are dividing one of the pentagonal faces of the graph into $11$ faces, such that the adjacent faces are undisturbed (they remain pentagonal). Such a division can be applied to any "base" ployhedron, so for example a base polyhedron with $16$ faces guarantees polyhedra with $10n+6$ faces, $n\ge 2$, as well.

Combining this result with @Kundor's implies that almost any even number of faces $\ge 12$ can be accessed. Only $14$ and $18$, which are not multiples of $4$ and too small to be reached via the $10$-face incrementation, require further analysis. For $18$ we have a planar graph corresponding to a polyhedron (basically a trigonal bipyramid where each face is divided in thirds) but for $14$ there are no planar graphs and thus no solutions!*

So the possible numbers of faces turn out to be $12$ and all even numbers greater than or equal to $16$.

*We prove the lack of a pentagonal 14-hedron by a pigeonhole argument. First observe that there must be $5×14/2=35$ edges, therefore from the Euler characteristic 23 vertices. The sum of all orders of these vertices is $2×35=70=(3×23)+1$, meaning there must be one order-4 vertex out of the 23, the rest being order-3.

Now draw the order-4 verrex. It is surrounded by four faces which together take up 16 of the edges and twelve additional vertices. Eight of the additional vertices must have another edge emerging from it, thus accounting for a total of 24 edges and 12 faces. The remaider of the polyhedron, closing up the "bottom" side, must have two faces supplying 11 additional edges — but the faces are pentagonal and thus can supply a maximum of only ten more edges. $\rightarrow\leftarrow$

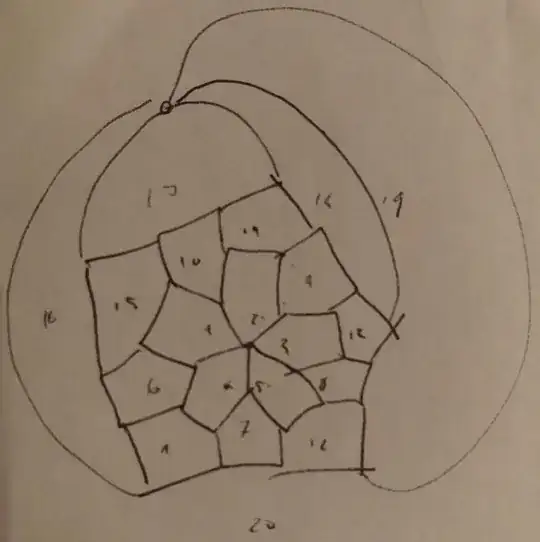
With 16 pentagonal faces the closure would have four faces and 16 edges, which is possible by constructing the second order-4 vertex existing in that case. This is Nick Matteo's construction.

Possible all-Pentagon Polyhedra

2 Answers2

Linked