3

I am reading book of abstract algebra. The proof of a lemma are as below. I am just wondering why is H of the special form: $a, a^2,... , a^{n +1}$?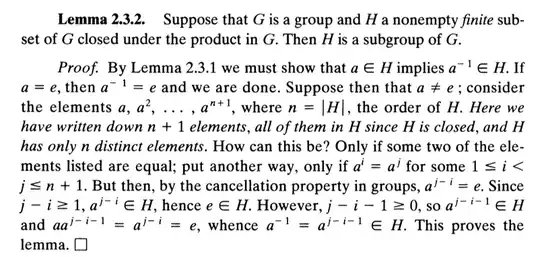enter image description here

user2262504
  • 994
  • 1
  • 14
  • 20
  • 2
    Pigeonhole Principle... – JP McCarthy Nov 26 '15 at 13:01
  • 2
    Just to be clear on this, many times, in a group $G$, when we want to prove something about an element $a$, we consider the subgroup generated by $a$. This usually tells us only something about $a$, but sometimes it can tell us something about $G$ as well. In this case, what the lemma has done is show that if $H$ is a finite subset of $G$ closed under multiplication, and $a \in H$, then $H$ contains the subgroup generated by $a$. To "fully" validate this, we have to repeat this for all the elements of $H$, but the way to do this should now be clear. – David Wheeler Nov 26 '15 at 13:33
  • 1
    they didn't say that $H$ is of that special form – Mirko Nov 26 '15 at 14:25
  • Just out of curiosity, which book is this result from? – Math Mar 11 '21 at 18:00
  • @Math should be "Abstract Algebra" by Herstein. – Maxwell Apr 29 '24 at 13:08

3 Answers3

8

Here is a simpler proof.

Let $a \in H$ and consider the map $\mu: x \mapsto ax$ on $G$.

$\mu$ sends $H \to H$ because $H$ is closed.

$\mu$ is injective because $G$ is a group. Hence, $\mu$ defines a bijection $H \to H$ because $H$ is finite.

Therefore, $au=a$ for some $u \in H$ and so $u=e$ and $e \in H$.

Also, $av=e$ for some $v \in H$ and so $v=a^{-1}$ and $a^{-1} \in H$.

lhf
  • 221,500
3

$H$ is not necessarily on the form $\{a,a^2,\ldots,a^{n+1}\}$.

You just pick an element $a\in H$ (such that $a\neq e$), and then you consider all the powers $a,a^2,\ldots,a^{n+1}$. These powers need not cycle through all elements of $H$.

It may very well be that they repeat themselves with a period of $2$, i.e. $a=a^3=a^5=\ldots$, and $e=a^2=a^4=\ldots$. There can be a lot of other stuff in $H$ besides the powers of $a$.

The only thing important to the proof is that you know that the powers repeat themselves at some point, which they will do, because there are $n+1$ of them, and $H$ only has $n$ elements.

Mankind
  • 13,500
0

The book does not say that $H$ is of the special form $\{a, a^2,... , a^{n +1}\}$.
All it says is that each $a^j$ is an $H$ and hence $\{a, a^2,... , a^{n +1}\}$ is a subset of $H$,
that is $\{a, a^2,... , a^{n +1}\}\subseteq H$.
It does not say that $\{a, a^2,... , a^{n +1}\}= H$.

Since $H$ has $n$ many elements, but $n+1$ many powers of $a$ are listed, then some of these powers of $a$ must coincide (the same element of the group is listed once as $a^i$ and listed later again, this time as $a^j$), that is $a^i=a^j$ for some $i,j$.

Mirko
  • 13,789