Claim. For any $x \in \Bbb{R}$ the limit is given by
$$ \lim_{n\to\infty} \sqrt{n} \sin^{\circ n}\left( \frac{x}{\sqrt{n}} \right) = \frac{\sqrt{3}x}{\sqrt{x^2+3}}. $$
Proof. To prove this, WLOG we assume that $x > 0$. Let $f_n(x) = \sqrt{n}\sin(x/\sqrt{n})$ and define
$$ x_{n;0} = x, \qquad x_{n;k+1} = f_n(x_{n;k}). $$
Also, for brevity, we suppress the dependence on $n$ to simply write $x_k = x_{n;k}$ unless we need it explicitly. Now using the inequality $|\sin \theta| \leq |\theta|$, we know that $|x_{k}| \leq |x|$ uniformly in $n$ and $k$. Then it follows that
\begin{align*}
\frac{1}{x_{n}^2}
&= \frac{1}{x^2} + \sum_{k=0}^{n-1} \left( \frac{1}{x_{k+1}^2} - \frac{1}{x_{k}^2} \right) \\
&= \frac{1}{x^2} + \sum_{k=0}^{n-1} \frac{(x_{k} - x_{k+1})(x_{k} + x_{k+1})}{x_{k}^2 x_{k+1}^2} \\
&= \frac{1}{x^2} + \sum_{k=0}^{n-1} \frac{\left( \frac{1}{6n}x_k^3 + \mathcal{O}(n^{-2}x_k^3 ) \right)\left( 2x_k + \mathcal{O}(n^{-1}x_k) \right)}{x_{k}^2 \left( x_k + \mathcal{O}(n^{-1}x_k) \right)^2} \\
&= \frac{1}{x^2} + \frac{1}{3n} \sum_{k=0}^{n-1} \left( 1 + \mathcal{O}(n^{-1} ) \right) \\
&= \frac{1}{x^2} + \frac{1}{3} + \mathcal{O}(n^{-1}).
\end{align*}
It is easy to check that $x_n = x_{n;n}$ is positive when $n$ is large. Consequently we obtain
$$ \lim_{n\to\infty} \sqrt{n} \sin^{\circ n}\left( \frac{x}{\sqrt{n}} \right)
= \lim_{n\to\infty} x_{n;n}
= \frac{\sqrt{3}x}{\sqrt{x^2+3}}. $$
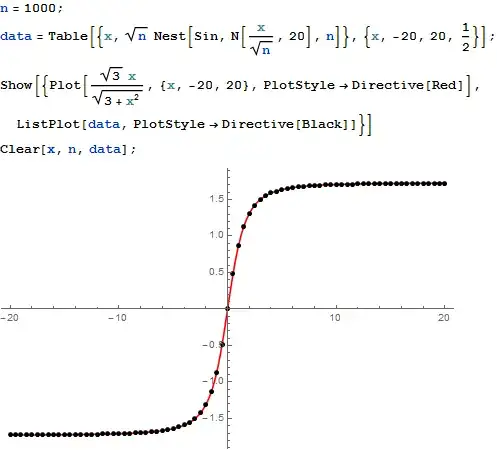
Addendum. The following is a numerical test with $n = 1000$ iterations: