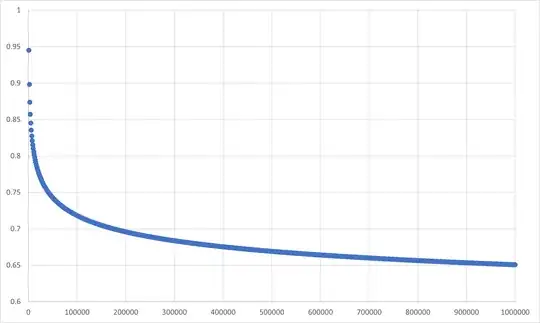
In this answer, we establish the following result:
$$ \bbox[color:navy;padding:8px;border:1px dotted navy;]{ \sinh^{\circ n}\sqrt{\frac{3}{n}} \sim \sqrt{\frac{5}{\smash[b]{\log n}}} \quad\text{as}\quad n \to \infty } \tag{$\diamond$} $$
The lemma below plays the key role in our analysis:
Lemma. Define $f(x) = \frac{3}{\sinh^2(\sqrt{3/x})}$. There exists a constant $C > 0$ such that
$$ x - 1 \leq f(x) \leq x \tag{1} $$
and
$$ x - 1 + \frac{3}{5x} - \frac{C}{x^2} \leq f(x) \leq x - 1 + \frac{3}{5x} \tag{2} $$
for all $x > 0$.
Let us first see how this lemma implies the main result. For each fixed $n$, we define $(n_k)_{0\leq k \leq n}$ so that $n_0 = 0$ and $n_{k} = f(n_{k-1})$ for all $1 \leq k \leq n$. This sequence is designed so that
$$ \sinh^{\circ k}\sqrt{\frac{3}{n}} = \sqrt{\frac{3}{\smash[b]{n_k}}}. $$
Then by $\text{(1)}$, for all $0 \leq k \leq n$ we have
$$ n - k \leq n_k \leq n. $$
Plugging this to the second part of $\text{(2)}$, for all $1 \leq k \leq n$ we get
\begin{align*}
n_k
&= n_0 + \sum_{j=0}^{k-1} (x_{j+1} - x_j) \\
&\leq n + \sum_{j=0}^{k-1} \left( -1 + \frac{3}{5(n - j)} \right) \\
&= n - k + \frac{3}{5}(H_n - H_{n-k}), \tag{3}
\end{align*}
where $H_m = 1 + \frac{1}{2} + \cdots + \frac{1}{m}$ is the $m$th harmonic number. Then plugging this to the first part of $\text{(2)}$,
\begin{align*}
n_k
&\geq n + \sum_{j=0}^{k-1} \left( -1 + \frac{3}{5(n - j) + 3(H_n - H_{n-j})} - \frac{C}{(n - j)^2} \right). \tag{4}
\end{align*}
Then from $(3)$, we have
$$ n_n \leq \frac{3}{5}H_n \sim \frac{3}{5}\log n. $$
Also, from $(4)$ and with $C' = C \sum_{k=1}^{\infty} \frac{1}{k^2}$, we get
\begin{align*}
n_n
&\geq \sum_{j=0}^{n-1} \frac{3}{5(n - j) + 3(H_n - H_{n-j})} - C' \\
&\geq \sum_{k=1}^{n} \frac{3}{5k + 3(\log n - \log k)} - C' \\
&\geq \int_{1}^{n} \frac{3 \, \mathrm{d}t}{5t + 3(\log n - \log t)} - C'.
\end{align*}
In the last step, we utilized $H_n - H_k = \frac{1}{k+1} + \cdots + \frac{1}{n} \leq \int_{k}^{n} \frac{\mathrm{d}t}{t} = \log n - \log k $ and the fact that $t \mapsto 5t - 3\log t$ is positive and increasing for $t \geq 1$. Then substituting $u = \frac{1}{\log n}\log t$,
\begin{align*}
n_n
&\geq (\log n) \int_{0}^{1} \frac{3 \, \mathrm{d}u}{5 + 3(1 - u)n^{-u}\log n} - C' \\
&\sim \frac{3}{5}\log n
\end{align*}
by the dominated convergence theorem. Therefore $n_n \sim \frac{3}{5}\log n$ and the desired conclusion follows by plugging this to $\sinh^{\circ n}\sqrt{\frac{3}{n}} = \sqrt{\frac{3}{\smash[b]{n_n}}}$. $\square$
Proof of Lemma. We assume $x > 0$ throughout this proof.
The second part of $\text{(1)}$ is the easiest one. From the inequality $\sinh t \geq t$ for $t \geq 0$, it follows that
\begin{align*}
f(x)
\leq \frac{3}{\left[ (3/x)^{1/2} \right]^2}
= x.
\end{align*}
Next, note that
$$ \sinh^2 t
= \frac{\cosh(2t) - 1}{2}
= \sum_{k=1}^{\infty} \frac{2^{2k-1}}{(2k)!} t^{2k}
\leq \sum_{k=1}^{\infty} \frac{1}{3^{k-1}} t^{2k}
= \begin{cases}
\frac{t^2}{1 - t^2/3}, & 0 < t < \sqrt{3} \\
\infty, & t \geq \sqrt{3}
\end{cases}. $$
Hence, $\frac{1}{\sinh^2 t} \geq \frac{1}{t^2} - \frac{1}{3}$ for all $t > 0$ and it follows that
$$ f(x) \geq 3 \left( \frac{1}{(\sqrt{3/x})^2} - \frac{1}{3} \right) = x - 1, $$
proving the second part of $\text{(1)}$.
Now we move on to proving $\text{(2)}$. The first part is evident from the asymptotic formula
\begin{align*}
f(x)
&= \frac{3}{\left[ (3/x)^{1/2} + \frac{1}{6}(3/x)^{3/2} + \frac{1}{120}(3/x)^{5/2} + \mathcal{O}(x^{-7/2}) \right]^2} \\
&= x - 1 + \frac{3}{5x} + \mathcal{O}(x^{-2}) \quad \text{as}\quad x \to \infty
\end{align*}
For the second part, from $ \sinh t \geq t + \frac{t^3}{6} + \frac{t^5}{120}$, $t \geq 0$, it follows that
\begin{align*}
f(x)
&\leq \frac{3}{\left[ (3/x)^{1/2} + \frac{1}{6}(3/x)^{3/2} + \frac{1}{120}(3/x)^{5/2} \right]^2} \\
&= x - 1 + \frac{3}{5x} - \frac{2200x^3 + 1365x^2 + 315x + 27}{5x (40x^2 + 20x + 3)^2} \\
&\leq x - 1 + \frac{3}{5x},
\end{align*}
completing the proof of the lemma. $\square$