Point of maximal error in the normal approximation of the binomial distribution

Question

I am sorry for the long question! Thanks for taking the time reading the question and for your answers!

Context: Let $B_n\sim\text{Binomial(n,p)}$ be the number of successes in $n$ Bernoulli trials of probability $p\in(0,1)$. Let $$\tilde B_n=\frac{B_n-np}{\sqrt{np(1-p)}}$$ be the standardized random variable and let $N\sim\text{N}(0,1)$ have the standardized normal distribution. Let $\epsilon_n(x)$ be the error between the cumulative distribution function of $\tilde B_n$ and $N$, i.e. $$\epsilon_n(x) = \left|\mathcal P(\tilde B_n \le x)-\mathcal P(N \le x)\right|$$

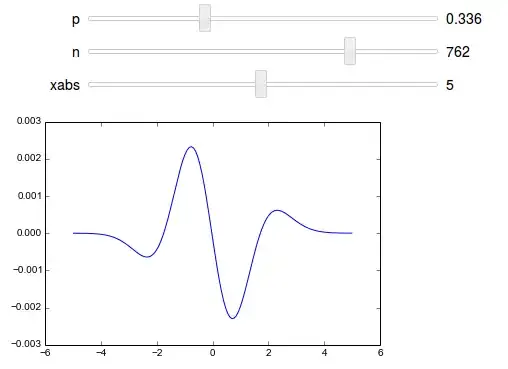
The central limit Theorem shows, that $\lim_{n\to\infty} \epsilon_n = 0$ (uniform in $x$). By doing numerical calculations I get always the result, that the supremum of $\epsilon_n$ is attained for $x\in[-1,1]$ (see below).

My question: Is there a proof, that the maximal error of $\epsilon_n(x) = \left|\mathcal P(\tilde B_n \le x)-\mathcal P(N \le x)\right|$ is always attained in the interval $x\in[-1;1]$, i.e. that the point $x$ where $\left|\mathcal P(\tilde B_n \le x)-\mathcal P(N \le x)\right|$ is maximal fulfills $-1\le x\le 1$? Is this true?

Some diagrams: Here is a plot of $f(x)=\mathcal P(\tilde B_n \le x)-\mathcal P(N \le x)$ for $p=0.336$ and $n=762$:

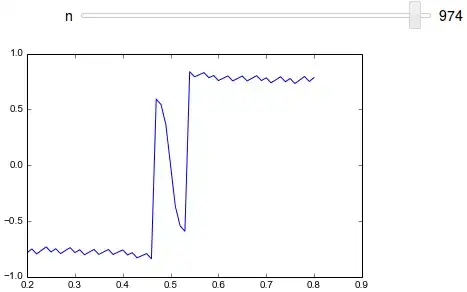
Here is a plot showing the position of the maximal error, i.e the point $x$ where $\epsilon_n(x)$ is maximal. On the x-axis is the value $p\in(0,1)$. The y-axis shows the point $x$ where $\epsilon_n(x)$ is maximal in the calculation:

You can see, that the maximal error is always attained for $-1\le x \le 1$.

Note: I know, that because $\mathcal P(\tilde B_n \le x)$ has steps, the function $\epsilon_n$ is not continuous and thus $\sup_{x\in\mathbb R}\epsilon_n(x)$ may not be attained. But as you can see in the diagram the preimage of a sufficiently small neighborhood of $\sup_{x\in\mathbb R}\epsilon_n(x)$ lies in $[-1;1]$...

This question is also related to my follow up question Normal approximation of tail probability in binomial distribution (which describes my motivations behind this question).

Answer 1

I noticed, that the diagrams are wrong (I'm sorry!). They do not show $P(\tilde B_n < x) -P(N \le x)$ but $P(\tilde B_n = x) -\phi(x)$ (the difference in the density functions).

So far I have the idea to use the Edgeworth series which states:

$$P(\tilde B_n\le x) = \Phi(x) - \frac 1{6\sqrt n} k_3 (x^2-1) \phi(x) + \frac{R\left(np+x\sqrt{npq}\right)}{\sqrt{npq}}\phi(x) + o\left(\frac 1{\sqrt n}\right)$$

with $R(x) = \lfloor x\rfloor -x+\frac 12$ and $k_3$ being the 3rd culmulant. I hope, that with this formula one can prove that the maximum of $\left|P(\tilde B_n\le x)-\Phi(x)\right|$ is attained around $x\approx 0$ (there lies the maximum of $|(1-x^2)\phi(x)|$ as well as of $\phi(x)$).

Reference for the formula:

• Peter Hall "The Bootstrap and Edgeworth Expansion", 1992, Springer series in statistics, page 46

Peter Hall cites here:

• Gnedenko and Kolmogorov (1954, Section 43): Limit Distributions for Independent Random Variables. Addison-Wesley