By generalizing methods used in An integral involving a Gaussian and a logarithm. I have computed the following integral below: \begin{eqnarray} \tilde{\mathcal I}(A) &:=& \int\limits_{-1/A}^\infty \log(1+A \xi) \frac{e^{-\xi^2/2}}{\sqrt{2\pi}} d\xi \\ &=& \frac{1}{2} \log(\sqrt{2} A)+\frac{1}{4} \psi(1/2) + \frac{1}{4 A^2} F_{2,2}\left[\begin{array}{rr} 1 & 1 \\ 3/2 & 2\end{array};-\frac{1}{2 A^2}\right] + \frac{\log(\sqrt{2} A)-\gamma/2}{A \sqrt{2 \pi}} F_{1,1}\left[\begin{array}{r} 1/2 \\ 3/2 \end{array};-\frac{1}{2 A^2}\right] -1/2 \frac{1}{A \sqrt{2\pi}} F_{1,1}^{(1,0,0)}\left[\begin{array}{r} 1/2 \\ 3/2\end{array};-\frac{1}{2 A^2}\right] \end{eqnarray} Here $\psi$ denotes the di-gamma function and $F_{1,1}^{(1,0,0)}$ is the derivative of the hypergeometric function with respect to its first parameter. Clearly $\tilde{\mathcal I}(A) \simeq -A^2/2$ as $A \rightarrow 0_+$ and $\tilde{\mathcal I}(A) \simeq 1/2 \log(A)$ as $A \rightarrow \infty$.
The quantity $\tilde{\mathcal I}(A)$ along with the real part of the quantity ${\mathcal I}(A)$ are plotted below in Red and in Blue respectively.
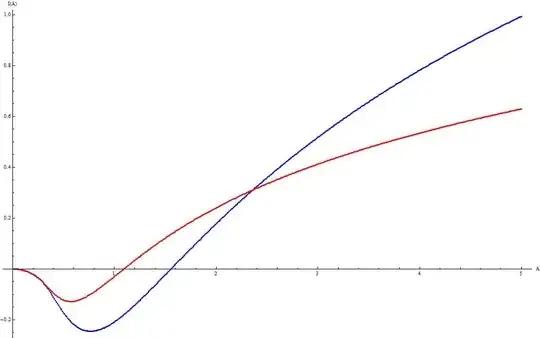
Now, again the question is how will the result look like is we replace the Gaussian by a Tsallis' or a L\'{e}vy stable density function ?