Aren't the eigenvalues of $\Gamma$ always $1\pm \frac{1}{\sqrt{2}}$? I'm confused as to why you're asking for asymptotics (and why you say this is only interesting for odd $n$).
If we express $\rho$ and $\sigma$ using coordinates in the $\omega$ basis, they are
$R=Q_R \Lambda Q_R^*$ and $S=Q_S \Lambda Q_S^*$ where
$$\Lambda = \left[\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right] = \Lambda_R = \Lambda_S$$
$$Q_R = \left[\begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right] = \frac{1}{\sqrt{2}}H_2$$
$$Q_S = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] = I_2$$
and $H_2$ is the $2\times 2$ Hadamard matrix.
$R$ has eigenvalues $\lambda_1$ and $\lambda_2$. $R^{\otimes n}$ has eigenvalues
$\lambda_1^i \lambda_2^{n-i}$ with $i\in {0,\ldots ,n}$ and multiplicity
$\left(\begin{array}{c} n \\ i \end{array} \right)$. ((Clarification: This lists the eigenvalues in increasing order; it is simply the
reverse of them in decreasing order. The multiplicities are correct regardless; the
binomial coefficients are symmetric. Note that neither of these orderings is the
order in which the eigenvalues appear along the diagonal of $\Lambda^{\otimes n}$.
See below.)) We also know the eigenvectors:
$$R^{\otimes n} = \left(Q_R^{\otimes n}\right) \left(\Lambda^{\otimes n}\right) \left(Q_R^{\otimes n}\right)^*$$
where
$$\begin{array}{rcl} Q_R^{\otimes n} &=& 2^{-n/2} H_2^{\otimes n} \\ &=& 2^{-n/2} \left[\begin{array}{cc} H_2^{\otimes n-1} & H_2^{\otimes n-1} \\ H_2^{\otimes n-1} & -H_2^{\otimes n-1} \end{array}\right]\end{array}$$
We also have that $S^{\otimes n} = \Lambda^{\otimes n}$ (and $Q_S^{\otimes n}=I_{2^n}$). Note using the Kronecker product here mirrors the Sylvester construction for (real) Hadamard matrices.
We know $\lambda_1^i \lambda_2^{n-i} > \lambda_1^j \lambda_2^{n-j}$ whenever $i>j$.
(I'm assuming that in addition to $\lambda_1>\lambda_2$ and $\lambda_1+\lambda_2=1$,
you also meant $\lambda_1,\lambda_2\geq 0$.) ((Clarification: This is correct as stated. Note this is purely an algebraic
statement about the $\lambda_i$'s. It has nothing to do with their being eigenvalues
or the ordering thereof.)) Then the eigenvectors of $R^{\otimes
n}$ with largest magnitude are always the first $2^{n-1}$ ones. For $R^{\otimes n}$,
that's $2^{-n/2} \left[\begin{array}{c} H_2^{\otimes n-1} \\ H_2^{\otimes n-1} \end{array}\right]$,
and for $S^{\otimes n}$, that's $\left[\begin{array}{c} I_{2^{n-1}} \\ 0 \end{array}\right]$.
That makes $B=2^{-n/2} H_2^{\otimes n-1}$. From your other
question
and my answer there, we know the eigenvalues of $\Gamma$ are $1\pm \sigma$ where
$\sigma$ is a singular value of $B$. But the singular values of $H_2^{\otimes n-1}$
are all $2^{(n-1)/2}$ so the singular values of $B$ are all $\frac{1}{\sqrt{2}}$.
That makes the eigenvalues of $\Gamma$ all $1\pm \frac{1}{\sqrt{2}}$.
A different example
A word of caution applies, though. Suppose for the sake of argument you allow $Q_R$
to be any orthonormal basis, $R$ to be of any dimension, and free yourself to choose
any columns of $Q_R$ to form $B$.
The columns of any (complex) Hadamard matrix represent a scaled version of a basis that is mutually
unbiased with respect to the standard basis. Also, if $H_n$ is a Hadamard matrix (of dimension
$n$), then so is
$$\hat{H}_{2n} = \left[\begin{array}{cc} H_n & H_n \\ H_n & -H_n \end{array}\right]$$.
(This is the Sylvester construction.)
If we are free to choose any columns we please in constructing $\Gamma$, then we can
always choose them from $\hat{H}_{2n}$ so that $\Gamma$ is singular. Pick $n/2$
columns from the first $n$ columns, and then pick corresponding columns from the
second $n$ columns: if the $i$th column is chosen, then also choose column $i+n$.
This doesn't meet one of your other criteria: that the columns chosen have their first-half components linearly independent. However, we can use the ideas above to construct columns whose first-halves are nearly dependent (as nearly singular as you choose). Let
$$H(\theta) = \frac{1}{2} \left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 1 & ie^{i\theta} & -1 & -ie^{i\theta} \\ 1 & -1 & 1 & -1 \\ 1 & -ie^{i\theta} & -1 & ie^{i\theta} \end{array}\right]$$.
This is a one-parameter family of (scaled) Hadamard matrices of order 4. The first principal
$2\times 2$ submatrix has singular values:
$$\sigma = \left\{\frac{1}{2} \pm \frac{1}{2\sqrt{2}}\left(1-\sin x\right)^{1/2}\right\}^{1/2}$$.
By choosing $\theta=-\pi / 2 + \epsilon$, we can make the lesser singular value vanishingly small , and the larger one arbitrarily close to 1.
For $\epsilon\ll 1$, the smaller singular value is approximately $\epsilon/4$ (and the larger is $1-\epsilon/4$).
This construction can be extended to higher dimensions. For example, the matrix
$$\left[\begin{array}{cc} H_{\theta} & H_{\theta +\epsilon} \\ H_{\phi} & -H_{\phi +\epsilon} \end{array} \right]$$
has columns 2, 4, 6, and 8 that are linearly independent and that have first halves that are linearly independent.
But, as above, the matrix $B$ of the first halves of these columns has singular values as close as desired to 0 or 1.
EDIT: OK. I've made a correction above along with a couple of clarifications. I've also replied to and expanded on the comments below.
As constructed above, the values along the diagonal of $\Lambda^{\otimes n}$ -- the
eigenvalues -- appear in binary order of the states. For $n=3$ this is: 000, 001,
010, 011, 100, 101, 110, and 111. This arises naturally out of the Kronecker
product ($\otimes$). However, it's not the order you're asking for. You say you want the states
sorted by Hamming distance from the
origin. For $n=3$ this is: 000, 001, 010, 100, 011, 101, 110, and 111. Note that
this ordering is ambiguous for even $n$ whereas the binary ordering is always
unambiguous.
You want $B$ to be a principal submatrix of a permutation (symmetrically of both the
rows and columns) of the Kronecker product/power $Q_R^{\otimes n}$. I'm not sure if
this has a name (and, of course, it's not the natural one that arises out of the
Kronecker product, the one I analyzed above). But now that I know what you're asking
for, I can recompute and edit this answer.
To restate the example in the comments below, for $n=3$ the binary order results in
$$2\sqrt{2}B = \left[\begin{array}{cccc}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{array}\right]$$
whereas the Hamming sort results in
$$2\sqrt{2}B = \left[\begin{array}{cccc}1&1&1&1\\1&-1&1&1\\1&1&-1&1\\1&1&1&-1\end{array}\right]$$
(which is unambiguous regardless of the subsort of 001, 010, 100).
EDIT: I haven't been able to find an analytic expression for the smallest
eigenvalue of $\Gamma$ for arbitrary $n$ nor an analytic expression for the
asymptotic value as $n$ gets large. However, I have been able to find a reduction of
the problem that allowed me to compute exact values up to $n=9$ and approximate
values up to $n=21$. I thought I'd post those results so you don't keep waiting.
As noted before, the smallest eigenvalue of $\Gamma$ is $1$ minus the largest
singular value (closest to $1$) of $B$. The right singular vector corresponding to
this value has the form
$\left[\begin{array}{cccccc}1&x_1&x_2&x_3&\cdots&x_{(n-1)/2}\end{array}\right]$ where
$1$ is repeated once, $x_1$ is repeated $n$ times, $x_2$ is repeated
$\left(\begin{array}{c}n\\2\end{array}\right)$ times, $x_3$ is repeated
$\left(\begin{array}{c}n\\3\end{array}\right)$ times, and so on. For the largest
singular value, the $x_n$'s are all positive. (Other singular vectors also have this
form, but not all do.) Using this ansatz, we can reduce the $2^{n-1}\times 2^{n-1}$ eigensystem for
$B$ down to a $\frac{n+1}{2}\times\frac{n+1}{2}$ system.
I was able to find exact values for $n$ equal to 3, 5, 7, and 9. The smallest
eigenvalue of $\Gamma$ is $1-2^{-n/2}\phi_n$ for $\phi_n$ in the following table:
$$\begin{array}{r|c}
n&\phi_n\\ \hline
3& 1+\sqrt{3} \\
5& 3+\sqrt{7} \\
7& 1+\sqrt{21}+\frac{1}{2}\sqrt{168-8\sqrt{21}} \\
9& \frac{1}{2}\left( \sqrt{2\sqrt{561}+462} + \sqrt{561} - 1 \right)
\end{array}$$
I was able to find approximate values up to $n=21$. The smallest eigenvalues are 3.4074e-2, 1.9627e-3, 8.5098e-5, 3.2961e-6, 1.2022e-7, 4.2208e-9, 1.443097e-10, 4.83855e-12, 1.5987e-13, and 5.28402e-15. If we make a log-log plot of them versus $m=2^n$, we get nearly a straight line:
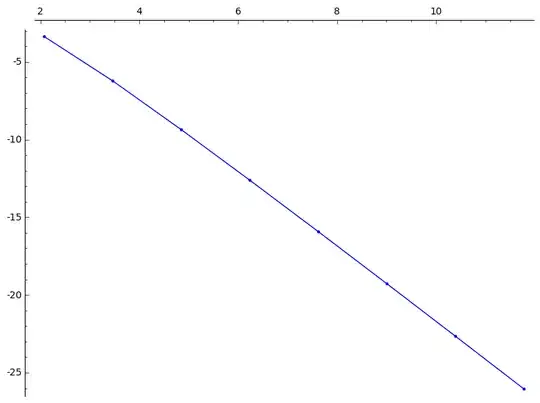
A fitted line gives $\lambda\approx Cm^{-2.5}$. This is monomial in $m$, but not in $n$ as you asked. In terms of $n$, this is $\lambda\approx C2^{-2.5n}$.
