1

What can we say about the determinant and (or) maximum eigenvalue of a matrix with entries equal to $1$ and $-1$. Further assume that the rows and columns are linearly independent. Are there special forms of such matrices where we can upper bound determinant and maximum eigenvalue of the matrix?

mich95
  • 8,935
James Smithson
  • 304

1 Answers1

0

Since you want to put bounds on the eigenvalues of such matrices, I think that using Gershgorin's Circle/Disc Theorem is helpful.

This theorem says that if $A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}$ and $\lambda$ is some eigenvalue of $A$, then

$$|a_{ii} - \lambda| \leq \sum_{j\neq i} |a_{ij}| \qquad \text{for $i = 1,2, \ldots, n$ }.$$

When plotting this information on the complex plane, we find that any eigenvalue of $A$ must be contained in the union of the circles whose centers are determined by $A$'s diagonal entries and whose radii are determined by the sum of magnitudes of the corresponding non-diagonal entries in that row.

Let's try an example from this html/powerpoint here:

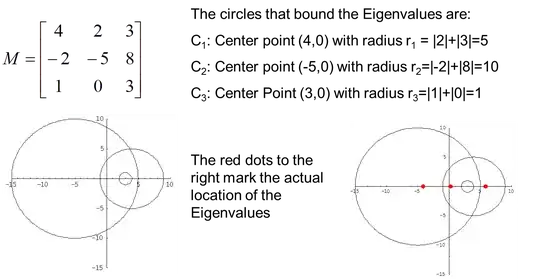
Example

Now in your case, you know that the rows and columns of your matrix will be linearly independent. By the Fundamental Theorem of Invertible Matrices, we know that your matrix will be invertible. So right away that is logically equivalent to saying that none of your matrix's eigenvalues will be zero. Also, you know that the determinant of such a matrix will also be non-zero.

As for the maximum eigenvalue, let $A$ be $n\times n$. You say that each entry is $\pm 1$ so then by Gershgorin's Circle/Disc Theorem, this means that in any given row $i$, $$|\pm1-\lambda| \leq \sum_{j\neq i}^{n} |\pm 1| = \sum_{j\neq i}^n 1 = (n-1).$$

You can draw the circles/discs associated with these inequalities fairly easily.

Furthermore, if you know that your matrix is symmetric, it can be shown that all of your matrix's eigenvalues are real. This means that instead of drawing circles in the complex plane and taking their union to bound the eigenvalues, you're really just taking the union of 1-dimensional intervals on the Real line.

I'm sure that more information about the determinant and bounds on eigenvalues exist beyond what I've presented above, but it's a start!

Xoque55
  • 4,499
  • Thank you for your response. I'm looking for sharper upper-bounds that $n-1$. Maybe you could have a look at this question: http://math.stackexchange.com/questions/1330576/determinant-of-a-certain-block-structured-positive-definite-matrix The upper bound I'm looking for will be useful in solving this question. As you can see matrix $B=\frac{1}{\sqrt{n}}A$ where $A$ is a (1,-1) matrix. So already we know that its maximum eigenvalue will be less than $\sqrt{n}$. – James Smithson Jun 30 '15 at 10:28