8

I read all posts online regarding how to show four points are coplanar. However, none of them discuss the idea behind the method. Can someone explain how the triple scalar product works?

LKSR
  • 555
  • 1
  • 5
  • 17

2 Answers2

14

You know that three points $A,B,C$ (two vectors $\vec{AB}$, $\vec{AC}$) form a plane. If you want to show the fourth one $D$ is on the same plane, you have to show that it forms, with any of the other point already belonging to the plane, a vector belonging to the plane (for instance $\vec{AD}$).

Since the cross product of two vectors is normal to the plane formed by the two vectors ($\vec{AB} \times \vec{AC}$ is normal to the plane $ABC$), you just have to prove your last vector $\vec{AD}$ is normal to this cross product, hence the triple product that should be equal to $0$:

$\vec{AD} \cdot(\vec{AB} \times \vec{AC})=0$

Stefan4024
  • 36,357
Martigan
  • 5,969
  • 3
    This is also equivalent to saying that the volume of the parallelepiped built on the vectors $AB, AC, AD$ is zero (because it is flat). – Mark Bennet Jun 18 '15 at 16:04
  • @MarkBennet This is true, but I think this is more advanced thinking and knowledge than just finding out normal vectors. – Martigan Jun 18 '15 at 16:15
  • Is it possible to just solve the equation of the plane ABC, then see if the other point D is included in that plane? I think it'll be simpler. – user3932000 Jan 17 '16 at 16:29
  • @user3932000 In fact this is the same. When you compute the triple product, you are doing as many calculus as finding out the equation and verifying that D belongs to the plane. – Martigan Jan 19 '16 at 11:37
0

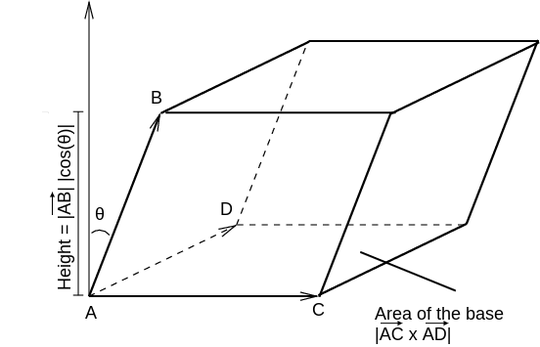
If you have 4 points A, B, C, and D. you can create $\vec{AB}$, $\vec{AC}$, $\vec{AD}$ vectors.

enter image description here

  • Area of the Base = $|\vec{AC} \times \vec{AD}|$
  • Height = $|\vec{AB}||\cos(\theta)|$
  • Dot Product Formula: $u \cdot v = |u||v|\cos(\theta)$
  • Volume = $|\vec{AC} \times \vec{AD}||\vec{AB}||\cos(\theta)| = |(\vec{AC} \times \vec{AD}) \cdot \vec{AB}|$

$\vec{AB}$, $\vec{AC}$, $\vec{AD}$ vectors will be coplanar if the volume of the parallelepiped is 0.

finally, the volume represents the triple scalar product which can be calculated as a Determinant:
if $\vec{AB} = \langle b_1,b_2,b_3 \rangle$ , $\vec{AC} = \langle c_1,c_2,c_3 \rangle$ , $\vec{AD} = \langle d_1,d_2,d_3 \rangle$ then:
$$ (\langle c_1,c_2,c_3 \rangle \times \langle d_1,d_2,d_3 \rangle) \bullet \langle b_1,b_2,b_3 \rangle = \begin{vmatrix} c_1 & c_2 & c_3 \\ d_1 & d_2 & d_3 \\ b_1 & b_2 & b_3 \end{vmatrix} $$

Sandro Skhirtladze
  • 121