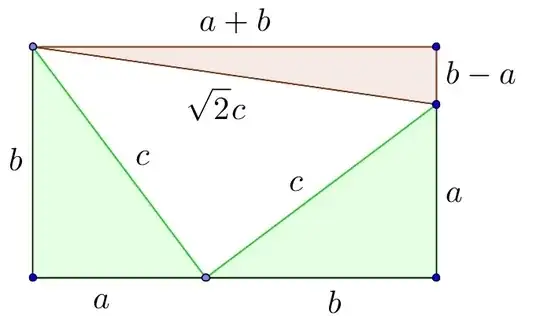
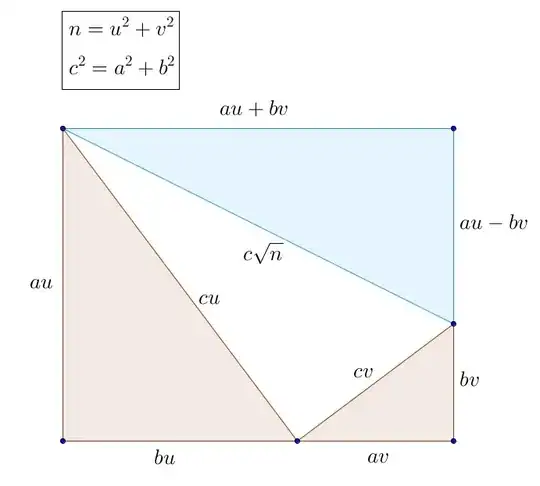
My question is does there exist a triple of integers, $a<b<c$ such that $b^2 = \frac{a^2+c^2}{2}$
I suspect that the answer to this is no but I have not been able to prove it yet. I realize this is very similar to the idea of Pythagorean triples but I am not versed enough in this subject to try and modify the theory for this case. One simple observation is that in order to have any hope of this working is that $a$ and $c$ must be of the same parity. Furthermore if such a triple exists we can build an infinite sequence since $(2b)^2 = \frac{(2a)^2+(2c)^2}{2}$ if and only if $b^2 = \frac{a^2+c^2}{2}$
Any help on determining this to be either true or false would be much appreciated. I am hoping it does end up being impossible, so if someone does find a desired triple I would next move up to cubes instead of squares
Edit: Thank you for the comments, I have foolishly overlooked a simple example and see that there are many solutions to this based on the theory of diophantine equations. However this is unfortunate for me because i was hoping NOT to be able to solve this. This question arose while studying a certain type of graph labeling. What I desire is to be able to create a sequence, $S$, of arbitrary length (since each member of the sequence is to be a label of a vertex in the graph) such that for every $x \in S$, $|x-s_i| \neq |x-s_j|$ for $ i \neq j$. I was naively hoping that the sequence of squares was sufficient to satisfy this condition.
Further edit, I have found that the sequence $2^n$ works but it would be nice if I could find a polynomial sequence.