Why do graphs sometimes have unevenly spaced intervals in axis e.g. logarithmic

Question

Why do some graphs not have evenly spaced out units on the x or y-axis? For example they have log on one or both of the axis?

Here's an example from this page

I guess the page does give a bit of an explanation which amounts to saying "with logarithmic scales the graph is more understandable" but doesn't it defeat the purpose of having a graph if you just make it look like a straight line? Now you're not reading numbers off a table but are reading the numbers off of the x and y-axis.

Here's another example where they do it

I have no clue how to tag this question.

Answer 1

A logarithmic scale can be used when the range of values in the independent/dependent variable is large, over several decades. This allows to observe the "infinitely small" at the same time as the "infinitely large".

Another benefit is that is allow to visually confirm intuition on the behavior of a law.

Indeed,

• $y=a\log x+b$ is a logarithmic law,
• $\log y=ax+b\equiv y=e^{ax+b}=BA^x$ is an exponential law,
• $\log y=a\log x+b\equiv y=Bx^A$ is a potential law.

So when you plot data in a semilogarithmic or bilogarithmic diagram and you get a perfect or a good alignment, you get a better insight on the relation. It is also easier to estimate the unknown coefficients from the straight line than from the original curve.

They say that this linearizes the relation.

Another use stems from the property $\log ab=\log a+\log b$: this turns multiplicative expressions into additive expressions, which can be easier to visualize and understand.

Answer 2

When you look at a chart for any particular stock on the NYSE, for example 3M Inc. (http://www.google.com/finance?q=mmm) try selecting zoom=all, and compare the difference between setting vertical scale = logarithmic vs. linear (click "settings" first). The apparent slope of the linear plot will tell you how quickly the nominal price of the stock is changing. The apparent slope of the logarithmic plot will tell you the relative (or percentage change) in price. The two types of plots are used differently. When monitoring the day-to-day fluctuations in price over the last several weeks is important, then we use a linear-linear plot. When analyzing the return-on-investment (ROI) over longer periods of time (possibly across decades), a logarithmic-linear plot is more useful.

Answer 3

Often the domain and the range of functions go over several orders of magnitude as in your examples; it would be not possible to represent them on a normal scale (look at your examples), so one uses different scales. It is not about making it look linear, but to get all the values in the diagram. Nonetheless in many cases you get linear relations between the logarithms.

See also:

http://en.wikipedia.org/wiki/Logarithmic_scale

Answer 4

Graphs are a wonderful tool. They help a skilled enough person fetch an enormous quantity of information in a glimpse.

Sometimes, though, a "normal" (read: linear) graph can be misleading or not sufficient. E.g.: say you have a function that grows very, VERY quickly. You need to estimate from visual data some satisfying enough information regarding the rate of growth.
Now, for an untrained eye, functions like $e^x$ and $e^{x^{x^x}}$ may even look similar, leading, in case we are using a linear graph, to some coarse approximation error.
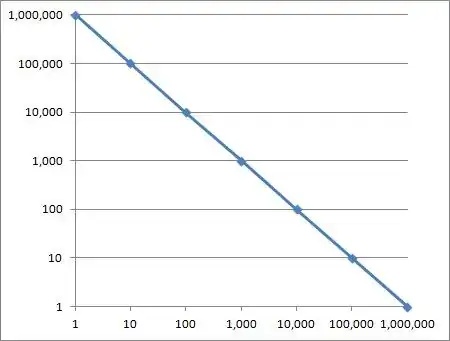
This cannot happen, though, if we use a log plot: here $e^x$ will look as a straight line, while $e^{x^{x^x}}$ is still gonna look like a fast-paced exponential-growing function. The pictures below represent said plots.

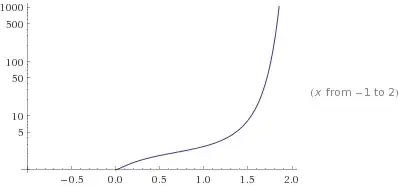
Of course, this is just one example, related to one of many different ways of representing data. Many others are possible, you just need to understand the context in which we use them.

Also, if you are into engineering, you might want to take a look to Bode plots. They are one of the most common examples of how a non-linear graph can help greatly the interpretation about data (in this case, concerning a system's frequency response).