Here's a good discussion of the "standard" answer to the problem, using one prisoner to "count" the others.
https://medium.com/i-math/100-prisoners-and-a-light-bulb-573426272f4c
The main difference from Levon's answer is that the counter isn't preselected, the first prisoner to enter the room becomes the counter. The group gets to start collecting counters slightly earlier that way.
The other nice thing about this article is it talks about a strategy for dealing with problems of this class. Imagine a simpler problem, reduce the 100 to something manageable (in the article's case, 5 prisoners).
Note that solutions for 1-3 prisoners are fairly trivial.
- 1 prisoner: leave after day 1
- 2 prisoners: leave if ever your first visit to the living room is not day 1
- 3 prisoners:
now incorporate light bulb
if your first visit is not day 1, turn the bulb on
if your first visit is not on day 1 and the bulb is on, then leave
For 4 prisoners, is there any faster approach than having the first prisoner become the counter? Can you use the regimes method at that level?
I wrote some short functions to benchmark the standard strategy.
import random
def generate_ledger(total_prisoners=100, ledger_length=200):
'''Generates a warden's ledger of randomly selected prisoners'''
ledger = []
for _ in range(ledger_length):
ledger.append(random.randint(0, total_prisoners-1))
return ledger
def freedom(ledger=[], total_prisoners=100):
'''Checks whether the prisoners, using the standard strategy, can escape
given a certain ledger'''
if len(ledger) < total_prisoners:
return False
counter = ledger[0] # The first prisoner is the counter
visited = set() # Set to keep track of prisoners who have turned on bulb
bulb = False # bulb starts off
visited.add(counter) # counter will visit first but never turn off own bulb
for prisoner in ledger[1:]:
# counter checks and turns off the light
if prisoner == counter:
if bulb:
bulb = False
# counter checks if all prisoners have visited
if len(visited) == total_prisoners:
return True
elif prisoner not in visited and not bulb:
visited.add(prisoner)
bulb = True
return False # If all prisoners didn't visit, return False
for ledger_length in range(6, 50):
# considers ledgers of lengths in range, testing total number of times
# in order to generate an estimate of success for the standard strategy
# against a random ledger of that length
count = 0
total = 10000
for i in range(total):
ledger = generate_ledger(total_prisoners=4, ledger_length=ledger_length)
if freedom(ledger, total_prisoners=4):
count += 1
print(f"ledger length {ledger_length}: {count}/{total}")
Output:
ledger length 6: 0/10000
ledger length 7: 11/10000
ledger length 8: 82/10000
ledger length 9: 199/10000
ledger length 10: 407/10000
ledger length 11: 730/10000
ledger length 12: 1129/10000
ledger length 13: 1566/10000
ledger length 14: 2184/10000
...
ledger length 23: 7166/10000
...
ledger length 26: 8270/10000
...
ledger length 30: 9155/10000
...
ledger length 33: 9508/10000
ledger length 34: 9574/10000
...
ledger length 41: 9920/10000
An alternative solution would divide the game into rounds of three and use parity bits. So each prisoner toggles the bulb on every odd visit they make to the room. On the fourth night, ...
[This version was non-optimal and confusing, removing in lieu of the TRY+TEST strategy.]
EDIT 16 MAY: The TRY+TEST Strategy
A simpler, more successful, and more generalizable strategy would be to leave the light on for prisoner D if all is well, turn it off if it's not.
So whoever arrives on day 1 is A, turns bulb on. If A returns day 2, turns bulb off, that round is a wash. If someone else arrives day 2, call him B, leave bulb on. For round three, if A or B returns, turn bulb off. Else C leaves on. On the next turn, if D sees a lit bulb, D knows all others visited. If unlit, someone visited twice and we must try again from scratch. You can vary this strategy by dividing each round into a "try" period for the first three days, then a "test" period where you're leaving the bulb on just waiting for D to arrive.
So you could have rounds of length 7, then at round_index % 7 == 0, you basically reset the state. A arrives and turns bulb on. %7==1, B leaves on, A turns off. %7==2, C leaves on, A or B turn off. %7 in [3-6], everybody ignores the bulb but D. Iff D sees a lit bulb, exits.
Implemented as follows:
def freedom_test_1(ledger=[], total_prisoners=4, round_length=7):
'''Checks whether the prisoners, using the alternate strategy, can escape
given a certain ledger
Turn bulb on / keep bulb on if ABC in beginning of round
Keep bulb on until D sees it or round resets
This time with greater lengths for D to check'''
# round_length = how long to check for D before giving up and resetting
OFF = False
ON = True
visitors = set()
bulb = OFF
for turn, prisoner in enumerate(ledger):
if turn % round_length == 0:
# reset state
visitors = set()
bulb = OFF
if turn % round_length in [0, 1, 2]:
if prisoner not in visitors:
visitors.add(prisoner)
bulb = ON
else:
bulb = OFF
else:
if prisoner not in visitors and bulb is ON:
return True
return False
So for round lengths of [6, 7, 8] I found these results:
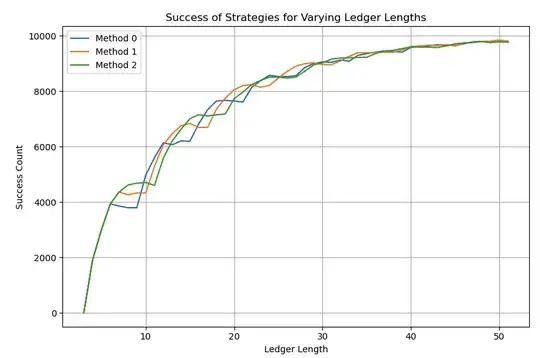
Adding the default "counter" strategy as Method 0 for comparison:
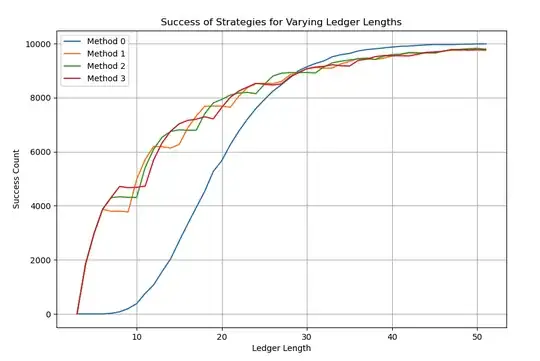
There are tradeoffs with round lengths on the try and test strategy, but it significantly outperforms counter until round lengths of 28 or so.

