0

I'm writing an article about a lecture that mentioned hyperbolic space. I wondered if anyone had a friendly way of describing it to the general public.

(I will rewrite any definitions in my own words, or credit you. No plagiarism here!)

ReidScience
  • 1
  • can you say more about the article, depending on what you are writing about different options exist, Is it about space time, Euclids 5th postulate, or about something else (and has nothing to do with hyperbolic geometry) – Willemien Feb 15 '15 at 12:08
  • Nothing that complicated! It's a summary of a lecture where the mathematician's work involved taking complex 3D objects and transforming them into hyperbolic (2D) space. This makes it easier to model mathematically. So I suppose I'd like a way of putting this idea into some sort of relatable context for readers. My own knowledge of hyperbolic space is that the sum of the angles of a triangle in hyperbolic space add up to less than 180 degrees. Wikipedia is far too advanced for me to make sense of. – ReidScience Feb 15 '15 at 16:25
  • I am one of the main editors of that wikipedia page (WillemienH) and I am trying to simplify the page a bit. btw you cannot really take any complex 3D objects and transforming it into hyperbolic space. Is your mathematician talking about an https://en.wikipedia.org/wiki/Pseudosphere ? – Willemien Feb 15 '15 at 17:11

1 Answers1

1

Most of the features of hyperbolic space already occur in dimension $2$.

One option is to use pictures of (uniform) tilings of the hyperbolic plane, and point out that, in hyperbolic geometry, the tiles are isometric and in particular have the same area.

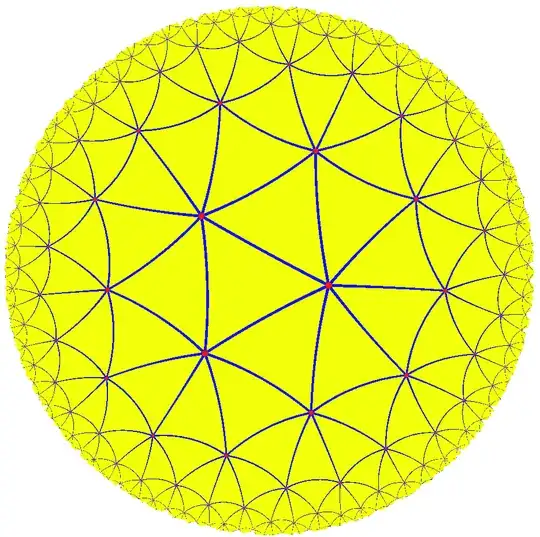
enter image description here

M. C. Escher drew four such tilings himself, all of them pretty. It might well be useful to contrast this with analogous tilings of the sphere and plane.

enter image description here

It would be illustrative to contrast hyperbolic plane with the sphere and plane in other ways too: For example, the circumference of a circle of radius $r$ is $2 \pi r$, less than $2 \pi r$ on a sphere (draw a picture!), and more than $2 \pi r$ on hyperbolic plane. Analogous statements are true for area and in higher dimensions.

Travis Willse
  • 108,056