To find number of distinct eigen values of this matrix

Question

I tried doing this with regular method and computations became very complex .Is there any shorter way , Am i missing something ?

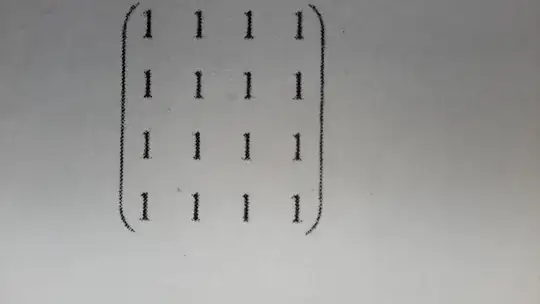
enter image description here

score 3 · Accepted Answer · answered Jan 11 '15 at 08:48

3

Hint: Since all columns (or alternatively all rows) all equal, the rank of the matrix is 1

answered Jan 11 '15 at 08:48

Droplet

Yes rank is 1 , so 0 must be an eigen value what about others ? – Sophie Clad Jan 11 '15 at 08:50
http://math.stackexchange.com/questions/146927/relation-between-rank-and-number-of-non-zero-eigenvalues-of-a-matrix Maybe this question can help – Droplet Jan 11 '15 at 08:54
So here M can have atmost 2 distinct eigen values , but how o che k whether it isone or two – Sophie Clad Jan 11 '15 at 08:58
You can use the fact that the trace (here 4) is also the sum of the eigenvalues – Droplet Jan 11 '15 at 09:04
1

Three eigen values here are zero which equals nullity so other will be 4 .Is that right ? – Sophie Clad Jan 11 '15 at 09:07
Yes, that's right. Congrats! – Droplet Jan 11 '15 at 09:12

score 2 · Answer 2 · answered Jul 18 '15 at 21:13

It can be done by using the characteristic equation:

Let us assume that the characteristic equaton of the matrix A is:

$$ \lambda^4 + a_1\lambda^3 + a_2\lambda^2 + a_3 \lambda + a_4 = 0$$

If you check then,

$$A^2 = 4 A$$

Using the fact that a matrix satisfies its own characteristic equation we get:

$$A^4 = 4 A^3 $$

Again writing it in terms of the Eigen values we get:

$$ \lambda^4 - 4 \lambda^3 = 0$$

Solve this and you will get two distinct Eigen values: 4 and 0.

2 Answers2