5

Evaluate:

$$\int_{0}^{\infty} \frac{\cos(x)}{x^2 + 1} dx$$

Using only complex analysis.

$$I = \int_{0}^{\infty} \frac{\cos(x)}{x^2 + 1} dx = (\frac{1}{2})\int_{-\infty}^{\infty} \frac{\cos(x)}{x^2 + 1} dx$$

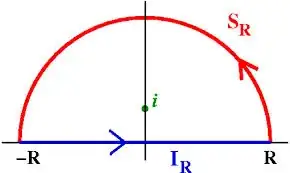
Consider a contour $C$ with a upper-axis semi-circle $B$ and the axis running from $-R \to R$

We will compute:

$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz$$

First:

$$z^2 + 1 = 0 \implies Z \in \{-i, i\}$$

Only, $z = i$ is in the semi circle region.

$$\text{Res}_{z=i} = \lim_{z \to i} (z-i)(f(i)) = \lim_{z \to i} \frac{\cos(z)}{z + i} = \frac{\cosh(1)}{2i}$$

Applying the residue theorem:

$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz = (2\pi i)\cdot \frac{\cosh(1)}{2i} = \pi\cdot\cosh(1)$$

$$\oint_{C} \frac{\cos(z)}{z^2 + 1} dz = \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2 + 1} dx$$

But that is wrong, the answer for the full improper is:

$$\int_{-\infty}^{\infty} \frac{\cos(x)}{x^2 + 1} dx = \frac{\pi}{e}$$

What am I doing wrong?

JohnD
  • 14,681
Amad27
  • 11,551
  • You seem to be confused about the use of $e^{iz}$ in the given answers. Read: http://en.wikipedia.org/wiki/Euler%27s_formula – Gahawar Dec 22 '14 at 14:59
  • I am aware of eulers formula. But it states: $e^{iz} = \cos(z) + i\sin(z)$ it includes $\sin(z)$ as well. Which is why you cant just substitute $e^{iz} = \cos(z)$ which is wrong. It is true that Re[$e^{iz}$] = $\cos(z)$ but how can we implement that looking at the contour top half of plane. – Amad27 Dec 22 '14 at 15:04

3 Answers3

5

The cosine function does not vanish on the semicircle as $R \to \infty$; in fact, it does the opposite. You need to either 1) take the real part of $e^{i x}$ in the upper half plane, or 2) use $\cos{x} = (e^{i x}+e^{-i x})/2$ and use both the upper and lower half planes, respectively.

Ron Gordon
  • 141,538
  • so I chose the wrong contour? Can you please address how to choose a contour here: http://math.stackexchange.com/questions/1077554/choosing-a-contour-to-integrate-over?

    It could help very much.

     – Amad27 Dec 22 '14 at 13:20
  • @Amad27: you didn't choose the wrong contour necessarily. You chose the wrong function to integrate over that contour. It seems to me, looking at your work, that you have omitted working out the piece that involves the integral over the semicircle. You really need to work it out to see what's going on. – Ron Gordon Dec 22 '14 at 13:21
  • But if we look at the function respectively. Should I have chosen a different contour? – Amad27 Dec 22 '14 at 13:22
  • @Amad27: please read my answer. If you choose option 1), then no, you don't have to. – Ron Gordon Dec 22 '14 at 13:23
  • What is the real "part" of $e^{ix}$? $e^{ix} = \cos(x) + i\sin(x)$ so, its still $\cos(x)$ – Amad27 Dec 22 '14 at 13:25
  • @Amad27: you write the cosine as the real part of the exp. The integral you seek is then the real part of the integral of exp divided by $1+x^2$. – Ron Gordon Dec 22 '14 at 13:26
  • I am unfamiliar with the "real part," terminology. What does that mean? What is the real part of $e^{ix}$? – Amad27 Dec 22 '14 at 13:28
  • Let us continue this discussion in chat. – Amad27 Dec 22 '14 at 13:28
  • 1
    @Amad27: actually, I'll pass. I'm a bit busy. If you're taking complex analysis and don't know what I am talking about, then you have some reading to do. – Ron Gordon Dec 22 '14 at 13:28
  • if you are free now, and have a minute, will you be able to guide me with one more question? $e^{ix} = \cos(x) + i\sin(x)$ if we use this as cosine, in our problem, it comes out incorrect? Because it also involves the sine into it. – Amad27 Dec 22 '14 at 15:21
5

we use $$f\left( z \right) = \frac{{e^{iz} }}{{1 + z^2 }}$$

sabachir
  • 422
  • 3
  • 5
1

we use $$f\left( z \right) = \frac{{e^{iz} }}{{1 + z^2 }}$$ then take real parts of the resulting integral .using the same contour $C$

enter image description here

\begin{array}{l} i \in C; - i \notin C \\ {\mathop{\rm Re}\nolimits} s\left( {f;i} \right) = \mathop {\lim }\limits_{z \to i} \left\{ {\left( {z - i} \right)\frac{{e^{iz} }}{{1 + z^2 }}} \right\} = \frac{{e^{ - 1} }}{{2i}} \\ \end{array} \begin{array}{l} \oint\limits_C {\frac{{e^{iz} }}{{1 + z^2 }}dz} = \int\limits_{ - R}^{ + R} {\frac{{e^{ix} dx}}{{1 + x^2 }}} + \int\limits_{S_R} {\frac{{e^{iz} dz}}{{1 + z^2 }}} = 2\pi i\frac{{e^{ - 1} }}{{2i}} = \frac{\pi }{e} \\ \Rightarrow \int\limits_{ - R}^{ + R} {\frac{{\cos \left( x \right)dx}}{{1 + x^2 }}} + i\int\limits_{ - R}^{ + R} {\frac{{\sin \left( x \right)dx}}{{1 + x^2 }} + } \int\limits_{S_R} {\frac{{e^{iz} dz}}{{1 + z^2 }}} = \pi e^{ - 1} \\ 2\int\limits_0^{ + R} {\frac{{\cos \left( x \right)dx}}{{1 + x^2 }}} = \pi e^{ - 1} ;\quad \left( {\int\limits_{S_R} {\frac{{e^{ix} dx}}{{1 + x^2 }} = 0} ;R \to + \infty \int\limits_{ - R}^{ + R} {\frac{{\sin \left( x \right)dx}}{{1 + x^2 }} = 0} } \right) \\ \mathop {\lim }\limits_{R \to + \infty } \int\limits_0^{ + R} {\frac{{\cos \left( x \right)dx}}{{1 + x^2 }}} = \frac{\pi }{2}e^{ - 1} \\ \end{array}

note: but if $y = {\mathop{\rm Im}\nolimits} \left( z \right)$ then $\cos \left( z \right) \approx \frac{{e^{\left| y \right|} }}{{\left| z \right|^2 }}$ for large $\left| z \right|$

we have the estimate $ \left| {\int\limits_{C_R } {\frac{{e^{iz} }}{{z^2 + 1}}dz} } \right| \le \int\limits_{C_R } {\frac{{e^{ - y} }}{{R^2 - 1}}\left| {dz} \right|} \le \frac{{\pi R}}{{R^2 - 1}} \to 0 $ as $R \to \infty $ where $ y = {\mathop{\rm Im}\nolimits} \left( z \right) > 0 $by the residue theorem $ \int\limits_{ - \infty }^{ + \infty } {\frac{{e^{ix} }}{{x^2 + 1}}dx = } 2\pi i\sum\limits_{{\mathop{\rm Im}\nolimits} a > 0} {{\mathop{\rm Re}\nolimits} s_a } \frac{{e^{iz} }}{{z^2 + 1}} = \frac{\pi }{e} $

Christian Fieldhouse
  • 889
sabachir
  • 422
  • 3
  • 5
  • how come you aren't using $\cos(z)$ ?? – Amad27 Dec 22 '14 at 14:43
  • @Amad27 $\cos(x)$ is the real part of $\exp(ix)$. So one should instead evaluate $\int_{-\infty}^{\infty}\frac{\exp(ix)}{x^2+1}dx$, and take the real part of this integral, in order to find the integral you want. – Angel Oct 25 '21 at 14:49