Is it a problem that "successful" machine learning algorithms have large VC dimension?

Question

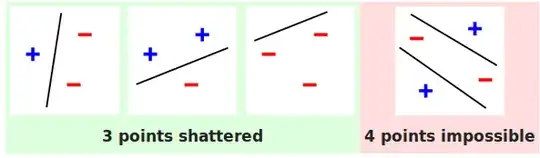
In my limited exposure, it appears that "successful" machine learning algorithms tend to have very large VC dimension. For example, XGBoost is famous for being used to win the Higgs Boson Kaggle competition, and Deep Learning has made many headlines. Both algorithm paradigms are based on models that can be scaled to shatter any dataset, and can incorporate boosting which increases VC dimension.

According to VC dimension analysis, a large dimension is supposedly a bad thing, it allows models to overfit or memorize the data instead of generalize. For example, if my model shatters every dataset, e.g. a rectangle around every point, then it cannot be extrapolated outside the dataset. My grid of rectangles tells me nothing about points outside the grid. The larger the VC dimension, the more likely the model will shatter a dataset instead of generalizing, and thus once exposed to new data outside the training dataset, it will perform badly.

Back to the original point, many of the most "successful" machine learning algorithms have this common trend of having a large VC dimension. Yet, according to machine learning theory this is a bad thing.

So, I am left confused with this significant discrepancy between theory and practice. I know the saying "In theory there is no difference between theory and practice, in practice there is" and practitioners tend to brush aside such discrepancies if they get the results they want. A similar question was asked regarding Deep Learning, and the consensus was that it did have large VC dimension, but that doesn't matter because it scores very well on benchmark datasets.

But, it is also said "there is nothing more practical than good theory." Which suggests such a large discrepancy has a significance for practical application.

My question then, is it true that the only thing that really matters is low error scores on test datasets, even when the theoretical analysis of the algorithm says it will generalize poorly? Is overfitting and memorizing instead of generalizing not that big of a deal in practice if we have hundreds of billions of samples? Is there a known reason why the theory does not matter in practice? What is the point of the theory, then?

Or, are there important cases where a very large VC dimension can come back to bite me, even if my model has great scores? In what real world scenario is low error and large VCD a bad thing, even with hundreds of billions of samples in the training data?

Answer 1

When left with a discrepancy between theory and data, data is king. Theory is intended to be predictive -- to make predictions about the world -- but when it fails to predict what we actually observe and experience, when its predictions disagree with our experience, then there is obviously something lacking in the theory.

In this case, VC theory just isn't adequate to understand modern practice in machine learning.

Unfortunately, VC theory ignores methods like regularization. Regularization is widely used in practice, so that's a pretty important gap in VC theory. VC theory counts the number (size, dimension) of possible models, and treats all of them as "equally valid/likely".

When we train a model with regularization, we depart from that paradigm. Regularization implicitly encodes the assumption that "all else being equal, simpler models (explanations) are more likely to be correct". In other words, regularization is essentially an application of Occam's Razor. In effect, regularization encodes some kind of prior on the distribution of likely models: not all models are equally likely; simpler models are more likely to be right. Classical VC theory doesn't take that into account, and thus can't make useful predictions about the behavior of machine learning methods that use regularization.

Practitioners aren't "brushing aside" the theory. Rather, VC dimension simply doesn't seem to be super-relevant to practice. It is too limited.

It's still an open question to understand why techniques like deep learning work so well. VC dimension was an early attempt to understand machine learning -- a powerful, beautiful, valiant attempt, one that may still be of some interest -- but ultimately one that doesn't seem to give us the whole picture, perhaps partly because it does not account for things like regularization and our priors on the model.

Answer 2

To expand my point in your previous post, VC theory (and PAC learning) is a WORST CASE theory. The requirement to handle any possible distribution on the data is too restrictive for real life applications. If $\mathcal{C}\subseteq 2^\mathcal{X}$ is a concept class with high VC dimension, there might still be an algorithm that achieves small generalization error relative to, say, the uniform distribution on $\mathcal{X}$. The question now is, whether the uniform distribution is something we can expect when treating examples from $\mathcal{X}$ (if for example I'm trying to separate pictures of dogs from pictures of cats, I wouldn't expect the uniform distribution on images to be meaningful here).

"Is it true that the only thing that really matters is low error scores on test datasets, even when the theoretical analysis of the algorithm says it will generalize poorly?"

Definitely not. It is useful to have an algorithm that seems to work, but you would be even happier if you could provide formal guarantees (error lower bound). We need some non worst case theory that finds the right conditions under which the algorithms you mentioned are indeed successful (in some formal sense), and argues why those conditions are satisfied in the cases where we witness empirical success. This will give us better understanding in general, and perhaps carve the way towards even better learning algorithms.