9

Good evening! I'm actually doing an internship at the Archives Nationales of France and I encountered a situation I wanted to solve using graphs...

I. The dusty situation

We want to optimize the arrangement of books of my library according to their height in order to minimize their archive cost. The height and thickness of the books are known. We already arranged the books in ascending order of height $H_1,H_2,\dots,H_n$ (I don't know if it was the best thing but... that's the way we did it). Knowing each book's thickness, we can determine for each $H_i$ class the necessary thickness for their arrangement, call it $L_i$ (for example, the books that are $H_i = 23\,\mathrm{cm}$ tall might have total thickness $L_i = 300\,\mathrm{cm}$).

The library can custom manufacture shelves, indicating the wished length and height (no problem with depth). A shelf of height $H_i$ and length $x_i$ costs $F_i+C_ix_i$, where $F_i$ is a fixed cost and and $C_i$ is the cost of the shelf per length unit.

Note that a shelf of height $H_i$ can be used to store books of height $H_j$ with $j\leq i$. We want to minimize the cost.

My tutor suggested I model this problem as a path-finding problem. The model might involve $n+1$ vertices indexed form $0$ to $n$. My mentor suggested I work out the existing conditions, each edge signification and how to work out the valuation $v(i,j)$ associated to the edge $(i,j)$. I would also be OK with other solutions as well as insights.

For instance we have for the Convention (a dark period of the French History) such an array:

\begin{array}{|c|rr} i & 1 & 2 & 3 & 4\\ \hline H_i & 12\,\mathrm{cm} & 15\,\mathrm{cm} & 18\,\mathrm{cm} & 23\,\mathrm{cm}\\ L_i & 100\,\mathrm{cm} & 300\,\mathrm{cm} & 200\,\mathrm{cm} & 300\,\mathrm{cm} \\ \hline F_i & 1000€ & 1200€ & 1100€ & 1600€ \\ C_i & 5€/\mathrm{cm} & 6€/\mathrm{cm} & 7€/\mathrm{cm} & 9€/\mathrm{cm}\\ \end{array}

II. The assumptions of a trainee bookworm

I think I have to compute an algorithm between Djikstra, Bellman or Bellman-Kalaba... I'm trying to find out which one in the following subsections.

1.Conditions

We are here with a problem of pathfinding between a vertex $0$ and a vertex $n$, $n$ must be outgoing from $0$ (that is to say, a path (or a walk) must exists between $0$ and $n$

2.What to compute (updated (25/10/2015))

// Work still under process as far as I don't know which vertices to and which edges to model...

My best guess

I think we get rid of at least one type of shelves every time we find a shortest path from the array, but that's only my assumption... ;).

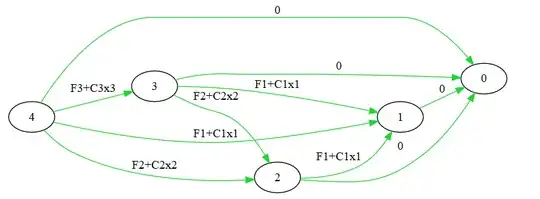
I think the best way to model how to buy shelves and store our books must look like the following graph, (but, please, feel free to criticize my method! ;))

from 0 graph

vertices:

  • $i\in[1,4]$ are shelves we can use to store our books.
  • $0$ is the state where no book is stored. Using this vertex allows me to use each cost formulas (edges).

edges: $F_i+C_ix_i,i\in[1,4]$ are the cost using a type of shelve. for instance: $F_1+C_1x_1$ fom 0 is the cost using only type 1 shelves to store our parchments, manuscripts...

Yet, from here I don't know how to create my shortest path problem.

Indeed, I would not know where would I have stowed all my books.

This leads me to another idea...

another idea...

to 0 graph

Here, I am searching for the shortest path from a given vertex to the 0 state, that is to say, knowing that the highest document is $type \ i$ tall, I am searching for the cheapest way to arrange my documents.

vertices:

  • $i\in[1,4]$ are shelves we can use to store our books.
  • $0$ is the state where all books are stored. Using this vertex allows me to use each cost formulas (edges).

edges: $F_i+C_ix_i,i\in[1,4]$ are the cost using a type of shelve. for instance: $F_1+C_1x_1$ from 3 is the cost using $type \ 1$ shelves after using $type \ 3$ shelves to store our parchments, manuscripts...

Yet, I don't know where to put $F_4+C_4x_4$.

3.How to compute

I think that we have to start with the higher shelves as far as we can then store the smaller books...

Do

We take $L_n$ cm of with the $H_{i=n}$ height in a shelve of their height + $z$ cm of an $H_{i=n-1}$ height until it becomes more expensive than taking the $H_{i=n-1}$ shelve. then $i=i-1$

While $i\neq0$

Finally, I don't know how to make $x$ varying...

That is to say how to choose to put $x_i$ documents in $4$ or $3$ for instance.

JimN
  • 891
  • 7
  • 22
Revolucion for Monica
  • 695
  • 1
  • 7
  • 20

3 Answers3

7

I think I have a solution to your problem. Hopefully I haven't misunderstood something in the definition of your problem. Here it goes:

I'm going to describe a Dynamic Programming approach. It's an $O(n^{2})$ algorithm, which means that since the number of books is huge it's not going to help you a lot. (you need to modify it a bit!). With some work, you can turn said Dynamic Programming approach into an instance of finding the shortest path on a Directed Acyclic Graph. (Which itself is a dynamic programming algorithm :P)

Suppose there are $n$ books all of different height.

Suppose also that the optimal cost is achieved by assigning the books to $i$ shelfs of height $h_{1},h_{2},...,h_{i}$ where $h_{1}<h_{2}<...<h_{i}$.

Let's prove the following two things:

A. $C_{a}>C_{a-1}$

Suppose the contrary. Let $B_{a-1}$ be the set of books assigned to shelf $a-1$ Then $cost = other,stuff + C_{a-1}*thickness(B_{a-1})$

Since, we assumed, $C_{a}<C_{a-1}$, let's transfer all books of shelf $a-1$ to $a$ (which is possible since $h_{a-1}<h_{a}$.

So,now, $cost =other,stuff + C_{a}*thickness(B_{a})$ which is lower than before. Hence, we have a contradiction due to the Optimality we assumed.

So $C_{a}>C_{a-1}$ for all shelfs created

B. Let $j$ be a book that is assigned to shelf $a$. Let's prove that $height(j)>h_{a-1}$

This is fairly easy. If $height(j)$ was smaller than $h_{a-1}$ we could put the book into shelf $a-1$ for a better cost (due to A).

Of the two things we've proven, B is the significant one.

Let $dp[a]$= the optimal cost for shelving books $1...a$ so that there is a shelf of $height(a)$. You have to find a way to define $dp[a]$ by the values $dp[1],dp[2],....dp[a-1]$

I'm going to stop here. If you are familiar with Dynamic Programming, using fact B, you will easily come up with the recurrence. Otherwise, ask :). As I said, this can be turned into a DAG problem. Knowing the relation above, it's easy to realize what the edge $(a,b)$ stands for and define its cost.

Last but not least, like I said above,as books are large, you cannot use the algorithm for each and every book. I think that representing its height by the sum of its thickness should do the trick. (I think it's already like that from your statement)

(I'm guessing number of different heights is much much less than number of books)

jjohn
  • 474
  • 3
  • 9
5

I see you as asking, "I want to solve this with Dijkstra's algorithm but I can't set up a good graph to run on," therefore I will present you with such a graph.

A digraph where vertices are sets of shelved books.

Okay, we have books with heights $H_n,$ $1 \le n \le N$ and widths $W_n,$ with heights in ascending order for each book, and we want to group them into shelves.

Reuse these numbers for solution nodes $n,$ where that node represents a solution state "all books $i \le n$ have been shelved." We will therefore start at node $0$ and seek to get to node $N$ by the shortest path with Dijkstra's algorithm. These nodes are the vertices of our graph.

We then draw from node $i$ to any node $j \gt i$ a directed edge which assumes that all of those intermediary books will be shelved with one shelf, i.e. the length of this edge is $$L_{ij} = F_j + C_j~\sum_{n=i+1}^j W_n,$$where I have assumed that when you were saying the cost of the sum was $F_i + C_i x_i$ the subscript $i$ on the $x_i$ was totally meaningless.

Dijkstra's algorithm will then give us a shortest-length path to node $N.$

CR Drost
  • 376
  • 1
  • 8
0

Sometimes just "zooming in" on the "nearest problem" in the literature can help understand the theory and background behind the problem, build an abstraction, and eliminate spurious details. The nearest problem in the literature to yours seems to be what is known as "variable size bin packing problem". Sample papers are included below. This problem is highly theoretically studied and some off-the-shelf software exists, it shows up in optimizing packing boxes in eg trucks shipping containers. There are also versions where one can adjust container size. There are many algorithmic approaches. eg, from 1st paper:

The problem addressed in this paper is that of orthogonally packing a given set of rectangular-shaped items into a minimum number of three-dimensional rectangular bins.

Community
  • 1
vzn
  • 11,162
  • 1
  • 28
  • 52