What's the longest period that an $n$-qubit Clifford operation can have?

Question

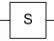
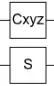
In https://arxiv.org/abs/2506.15147 , high-period constant-depth Cliffords are used to catalyze Z rotations. For an $n$ qubit state, the paper uses a Clifford with period $2^n-1$ built entirely out of CNOT gates.

Ignoring the constant depth requirement, is it possible to achieve much higher periods? The state space of an $n$ qubit stabilizer state isn't described by $n$ bits, it's described by $O(n^2)$ bits, so it seems conceivable that periods like $2^{(n^2)}$ could be achievable.

Note I don't consider global phase to be part of the period. If $C^3 = iC$, that's a period 3 operation.

I brute force searched solutions for n=1,2.

For $n=1$ the maximum period is 4 (e.g. the S gate).

For $n=2$, the maximum period is 12. Interestingly this can be achieved without any two qubit gates, by combining single qubit gates with periods of 3 and 4:

I sampled 100k random tableaus for $n=3,4,5,6$ and got:

for $n=3$ a period 24:

stim.Tableau.from_conjugated_generators(
    xs=[
        stim.PauliString("-XZX"),
        stim.PauliString("-X_X"),
        stim.PauliString("+YZZ"),
    ],
    zs=[
        stim.PauliString("-_YX"),
        stim.PauliString("+ZY_"),
        stim.PauliString("+YZY"),
    ],
)
q0: -X-@-X-@-X-X---------------
     | | | | | |
q1: -@-X-@-|-@-|-H-S-X---------
           |   |     |
q2: -----S-X-H-@-----@-S-H-S-S-

for $n=4$ a period 60:

stim.Tableau.from_conjugated_generators(
    xs=[
        stim.PauliString("-_ZYZ"),
        stim.PauliString("-ZYYY"),
        stim.PauliString("+ZXZ_"),
        stim.PauliString("-YYZ_"),
    ],
    zs=[
        stim.PauliString("+YYZY"),
        stim.PauliString("-_ZY_"),
        stim.PauliString("-XYX_"),
        stim.PauliString("+Y_YZ"),
    ],
)
q0: -X-@-X-H-@-@-@---X-X-------------------------------------------S-S-----
     | | |   | | |   | |
q1: -|-|-|-H-X-|-|---|-|-X-@-X-S-H-S-@-@-----------------------------------
     | | |     | |   | | | | |       | |
q2: -@-X-@-----X-|-H-@-|-|-|-|-----S-X-|-X-@-X-H-@---X-----H-S-S-H---S-S---
                 |     | | | |         | | | |   |   |
q3: -------S-----X-H---@-@-X-@-----S---X-@-X-@-S-X-H-@-S-H-S-H-S-S-H---S-S-

and for $n=5$ a period 120:

stim.Tableau.from_conjugated_generators(
    xs=[
        stim.PauliString("-_XZ_Y"),
        stim.PauliString("-ZY_YZ"),
        stim.PauliString("+XZZYZ"),
        stim.PauliString("-ZZ__X"),
        stim.PauliString("-XZZ_Z"),
    ],
    zs=[
        stim.PauliString("+XXX__"),
        stim.PauliString("+Y_Y_Z"),
        stim.PauliString("-Y_YXZ"),
        stim.PauliString("-YYX_Y"),
        stim.PauliString("+_ZYX_"),
    ],
)
q0: -X-@-X-H-S-@-@---X-X-X-X-----------------------------------------------------S-S-------
     | | |     | |   | | | |
q1: -@-X-@-----|-|-H-@-|-|-|-X-@-X-S-H-@-----X-X-----------------------H-S-S---H---S-S-----
               | |     | | | | | |     |     | |
q2: -----------X-|-S-H-@-|-|-@-X-@-----|-S-H-@-|-H-S-X-X---------------H---S-S-H-----S-S---
                 |       | |           |       |     | |
q3: ---------S---X-S-H---@-|-----------|---H---@---H-@-|-X-@-X-H-S-@---X-H---S-S-H-----S-S-
                           |           |               | | | |     |   |
q4: -----------------------@---------S-X-----------S-H-@-@-X-@---S-X-H-@-------------------

for $n=6$ the largest sampled period was 204:

stim.Tableau.from_conjugated_generators(
    xs=[
        stim.PauliString("+XZYZZY"),
        stim.PauliString("-_YYXZY"),
        stim.PauliString("+ZXZZ_X"),
        stim.PauliString("+YZY_ZZ"),
        stim.PauliString("-Y_ZZZY"),
        stim.PauliString("-YZY__Z"),
    ],
    zs=[
        stim.PauliString("+YXY_ZX"),
        stim.PauliString("+___Z__"),
        stim.PauliString("+_YZZ__"),
        stim.PauliString("+YY__XX"),
        stim.PauliString("+X____Y"),
        stim.PauliString("+ZZX_XX"),
    ],
)
q0: -S-H-S-@-@-@-@---X-X-X-----------------------------------------------------------H-S-S-H-S-S-----
           | | | |   | | |
q1: -------|-|-|-|---|-|-|-X-@-X-S-@-@---X-X-X-X-----------------------------------------------S-S---
           | | | |   | | | | | |   | |   | | | |
q2: -----H-X-|-|-|---|-|-|-@-X-@-H-X-|-H-@-|-|-|-X-@-X---@---X-X---------------------H---S-S-H---S-S-
             | | |   | | |           |     | | | | | |   |   | |
q3: -----S---X-|-|-H-@-|-|-----------|-H---@-|-|-|-|-|-H-X-H-@-|-X-@-X-@-----------------------------
               | |     | |           |       | | | | |         | | | | |
q4: -----H-----X-|-S-H-@-|-------S---X-H-----@-|-|-|-|---------|-|-|-|-|-X-@-X-H-@-------------------
                 |       |                     | | | |         | | | | | | | |   |
q5: -----S-------X-------@-------------H-------@-@-X-@---------@-@-X-@-X-@-X-@-H-X-S-H---------------

...which to my eye doesn't look like $2^{\Theta(n^2)}$ growth. Is there a proof it's not?

Answer 1

TL;DR: It turns out that $R_n = 2^{\Theta(n)}$ where $R_n$ is the maximum order of an $n$-qubit Clifford. More precisely, we find lower and upper bound \begin{align} 2^{\lfloor n/2 \rfloor} - 1 \leqslant R_n \leqslant 2^{2n+1} - 1 \tag1 \end{align} which follow from the fact that the maximum order of an element of $GL(k,\mathbb{Z}_2)$ is $2^k-1$.

Binary encoding for Pauli and Clifford operators

Let $\mathcal{P}_n$ denote the set of $n$-qubit Pauli operators with real eigenvalues$^1$ and $\mathcal{C}_n$ the projective$^2$ group of $n$-qubit Clifford operators which act on the set $\mathcal{P}_n$ by conjugation. We encode Pauli operators as bit strings using the bijection $b: \mathcal{P}_n \to \mathbb{Z}_2^{2n+1}$ that sends \begin{align} (-1)^rX^{x_1}Z^{z_1}\otimes\ldots\otimes X^{x_n}Z^{z_n} \in \mathcal{P}_n \tag2 \end{align} to $rx_1\ldots x_nz_1\ldots z_n \in \mathbb{Z}_2^{2n+1}$. We encode the action of Clifford operators on $\mathcal{P}_n$ as invertible matrices over $\mathbb{Z}_2$ using the injective homomorphism $M: \mathcal{C}_n \to GL(2n+1, \mathbb{Z}_2)$ that satisfies \begin{align} Q=CPC^\dagger \iff b(Q) = M(C) b(P) \tag3 \end{align} (and underpins stabilizer simulators). See e.g. this paper for details.

Note that the bit $r$ which accounts for the overall sign of a Pauli operator is necessary$^3$ for $M$ to be injective and hence order-preserving.

Maximum order binary matrix

For a positive integer $k$, let $A_k \in GL(k, \mathbb{Z}_2)$ denote any invertible matrix with the maximum possible order $2^k-1$ described in this answer which Sam Jaques pointed out in the comments.

Proof of lower bound

For any $B\in GL(k,\mathbb{Z}_2)$, define the $2k$-qubit unitary $U_B$ by \begin{align} U_B|x\rangle|y\rangle = |x\rangle|y\oplus Bx\rangle. \tag4 \end{align} The order of $B$ is the same as the order of $U_B$. Moreover, $B$ can be realized using CNOT gates only, so $U_B \in \mathcal{C}_{2k}$. Therefore$^4$, $U_{A_{\lfloor n/2 \rfloor}} \in \mathcal{C}_n$ is a Clifford unitary of order $2^{\lfloor n/2 \rfloor}-1$. $\square$

Proof of upper bound

By the answer linked to above, the order of every element of $GL(2n+1,\mathbb{Z}_2)$ is at most $2^{2n+1}-1$. In particular, the order of every element of the image $M(\mathcal{C}_n) \subset GL(2n+1,\mathbb{Z}_2)$ is at most $2^{2n+1}-1$. But $M$ is an injective homomorphism and hence order-preserving, so the order of any $C\in\mathcal{C}_n$ is at most $2^{2n+1}-1$. $\square$

Intuition

The idea to look at the order of binary matrices in order to compute or bound the order of Clifford unitaries has been inspired by the fact that simulation of stabilizer circuits and solving linear systems over $\mathbb{Z}_2$ are both $\oplus L$-complete, see complexity Zoo.

Possible improvement

The lower bound may be improved by manipulating the phase angles in $(4)$. For example, $\gcd(4, 2^{\lfloor n/2 \rfloor}-1)=1$, so a single $S$ gate on a qubit in the $|x\rangle$ register improves the lower bound to $2^{\lfloor n/2 \rfloor + 2}-4$.

---

^{$^1$ In other words, we reject Pauli strings with imaginary phase. Note that $\mathcal{P}_n$ is not a group.
$^2$ Projective Clifford group $\mathcal{C}_n$ is the quotient of the subgroup of $U(2^n)$ that fixes $\mathcal{P}_n$ under conjugation by its center, aka the global phase, $U(1)$. This choice of definition is explicit in the question, is physically reasonable (since global phase is unobservable), renders the group finite, and is needed to make $M$ injective.
$^3$ Consider for example $M(I)$ and $M(X)$.
$^4$ Pad with an extra qubit for odd $n$.}