In this post about 100 qubit fault tolerant devices it is stated that a system with 100 spin orbitals (or 50 spatial orbitals) is small enough that classical-computer algorithms can currently do the same calculations. But what if we use first quantization algorithms on a device with 200 logical qubits. An IBM CTO says that before the end of this decade we will have a 200 qubit device using LDPC codes and Gross codes ibm-cto-says-codes-and-commitment-are-critical-for-hitting-quantum-roadmap-goals
According to this paper: Quantum simulations of chemistry in first quantization even 200 logical qubits will not do much.
Fortunately, this is not the end of the story, in the case you want to simulate bigger molecules. LCU First quantization will cut the logical‑qubit footprint by an order of magnitude. For a diamond with a 64‑atom super‑cell (384 valence electrons, 32 768 dual‑plane‑wave orbitals) we need 6000 qubits instead of 60000. An 8 atom diamond requires less than 800 logical qubits. Simulating with high presision might be possible before 2030. I put some data from the paper in a plot.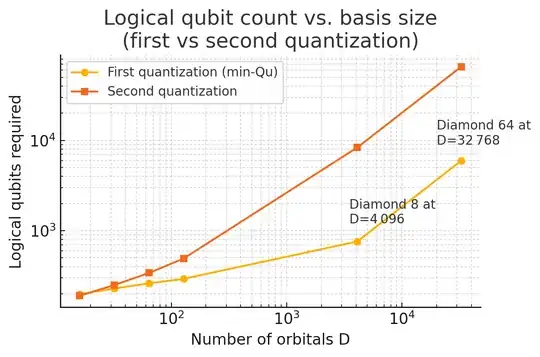 
Data points combine the medium‑scale Fe₂S₂ and the large diamond super‑cells taken directly from the paper’s Table 2 and Table 4. First and second quantisation algorithms use the same number of qubits for small Hamiltonians. Starting from about 200 qubits first quantization wins the batle. Once we are beyond a threshold first quantisation can help to make quantum advantage possible. Below 200 logical qubits there is not much difference between the red and orange lines, furthermore classical simulation beats quantum simulation. Between 200 and 800 qubits first quantization simulation becomes more performant. In the paper the authors show a LCU simulation and i will try to simulate a qiskit toymodel in another post. So given logical qubits and first quantization quantum advantage chemistry simulation might be possible before the year 2030?
Methode: Pauli LCU for first quantization.
The authors present an construction of the Hamiltonian as a linear sum of Pauli chains. This “Pauli LCU” allows the determination of the energy properties via qubitization and quantum phase estimation (QPE).Crucial is the storage (PREP) and selection (SELECT) of the non-zero LCU coefficients. They use sparse data techniques for this, so-called quantum read-only memory (QROAM), which provides a favorable trade-off between qubit and gate complexity.
