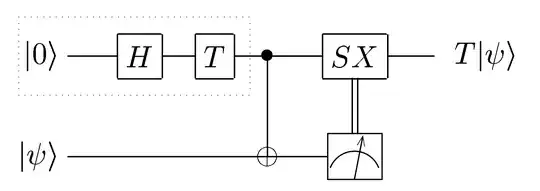
How is $Rx(\pi/2)$ applied to a qubit via state injection?

Question

In High threshold universal quantum computation on the surface code VI(C), Injecting $Rx(\pi/2)$ is claimed to be done with the following circuit

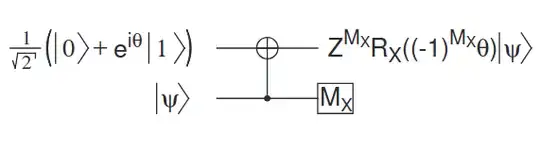
The paper says that if we want to do $Rx(\pi/2)$, we might have done $ZRx(-\pi/2)$ instead. This can be corrected by applying a Z followed by an X gate.

I do not get an $Rx(\pi/2)$ gate when I simulate this circuit and apply the recommended corrections. Below is the circuit that I believe follows what the paper is saying (with an $Rx(\pi/2)$ tacked on at the end in order to on the whole be perform an X gate so that we can see the gate's effects in the results).

0: ───H───S───X───────────Z───X───Rx(0.5π)───M('qubit')───
              │           ║   ║
1: ───────────@───H───M───╫───╫───────────────────────────
                      ║   ║   ║
a: ═══════════════════@═══^═══^═══════════════════════════

import cirq
import numpy as np
qubits = cirq.LineQubit.range(2)
c = cirq.Circuit(
    cirq.H(qubits[0]),
    cirq.S(qubits[0]),
    cirq.CX(qubits[1], qubits[0]),
    cirq.H(qubits[1]),
    cirq.measure(qubits[1], key='a'),
    cirq.Z(qubits[0]).with_classical_controls('a'),
    cirq.X(qubits[0]).with_classical_controls('a'),
    # Tack on this RX(pi/2) so an X gate is performed
    cirq.rx(np.pi/2).on(qubits[0]),
    cirq.measure(qubits[0], key='qubit'))
results = sim.run(c, repetitions=100).histogram(key='qubit')
print(results)

This prints Counter({0: 100}) when the expected answer should be Counter({1: 100}). This circuit seems to be performing an $Rx(-π/2)$ gate instead of an $Rx(π/2)$ gate. Is that right?

Do a Phase Flip · Answer 1 · 2025-04-10T07:08:30.070

The very first circuit diagram you show seems to be implementing the $R_X({\pi/2})$ gate through teleportation correctly. The issue seems to come from the gates you apply to bring your state back to the initial $|\psi\rangle$.

The last set of gates you. want to apply there is going to be: $$U^{\dagger} = \bigg(Z^{M_X}R_X\Big((-1)^{M_X}\theta\Big)\bigg)^{\dagger} = R_X\Big((-1)^{M_X}\theta\Big)Z^{M_X},$$ However, the implementation of the gate in cirq is not direct because the rotation is $\pm\frac{\pi}{2}$, meaning if the measurement is $0$ you apply $R_X\Big(\pi/2\Big)$ and if it's $1$, you apply $R_X\Big(-\pi/2\Big)$. This should result in the following circuit (checking that the output state is equal the initial (bottom) state:

# Test teleportation gate
qubits = cirq.LineQubit.range(2)
c = cirq.Circuit(
    # Initialise in |S> state qubit[0]
    # qubit[1] is in |0>
    cirq.H(qubits[0]),
    cirq.S(qubits[0]),
    cirq.CX(qubits[1], qubits[0]),
# X-basis measurement
cirq.H(qubits[1]),
cirq.measure(qubits[1], key='a'),

# Bring back the state to the inital |ψ&gt; state
# Classically controlled Z
cirq.Z(qubits[0]).with_classical_controls('a'),
# Rx((-1)^m pi/2)
cirq.rx(np.pi).on(qubits[0]).with_classical_controls('a'),
cirq.rx(np.pi/2).on(qubits[0]),

cirq.measure(qubits[0], key='qubit')

)
sim = cirq.Simulator()
results1 = sim.run(c, repetitions=100).histogram(key='qubit')
print(f"Teleportation circuit: {results1}")

Also note that the gates are applied from right to left in the matrix notation, but left to. right in the circuit notation.

Since the literature is a bit more developed on implementing these types of gates in the $Z$-basis (to implement phase $S$ and $T$ gates) you can change the basis one-to-one using $H$. A good example is given in this paper, they give a clear construction of the $T$-teleportation. You can do the exact same for the $S$ gate (= $T^2$) and then change the basis for your specific purpose. The figure is extracted from the same paper (14). Note that they also detail fault tolerant gate implementation using the cliffod gate hierarchy.

How is $Rx(\pi/2)$ applied to a qubit via state injection?

1 Answers1