Why no $Z$'s in the $\operatorname{F} (\sum_{j=0}^{n-1} 2^j Z_j) \operatorname{F}^\dagger$ operator?

Question

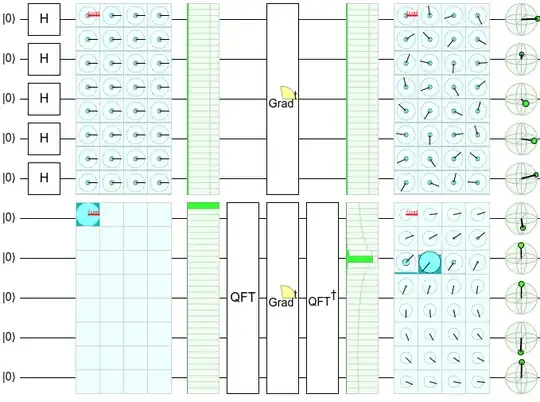
An interesting numerical observation is that an operator defined as $\phi=\sum_{j=0}^{n-1} 2^j Z_j$ upon a QFT is rotated into an operator $\pi=\operatorname{F} \phi \operatorname{F}^\dagger$ which does not have any Pauli $Z$'s in its expansion. Is there any simple way to understand this? While $\pi$ is off-diagonal, this is not a sufficient to lack any $Z$'s in its expansion.

Answer 1

When you conjugate a phase gradient with Fourier transforms, you get the offset operation $|k\rangle \rightarrow |k+x \pmod{2^n}\rangle$ where $x$ increases as the strength of the gradient increases. This relationship is a well known property in signal processing (shifts in the time domain become phase gradients in the frequency domain, and vice versa). It's also the key insight behind Draper's QFT adder.

Here's a Quirk circuit showing this off: