How to analyse a quantum circuit with an uncertain gate F?

Question

The following quantum circuit consists of two CNOT gates in the middle of the circuit. The two-qubit input quantum register $|x\rangle$ is an arbitrary quantum state and can be set by the user. The other two-qubit input quantum register $|00\rangle$ is in the ground state and cannot be changed. The gate $F$ is an unknown quantum operation (this means it is an arbitrary, but fixed gate on two qubits, but you do not know what it does). The gate $F^{-1}$ computes the inverse operation of $F$.

So how does this circuit work? Label the qubits from top to bottom as q1, q2 for the input $|x\rangle$ and q3, q4 for the input $|00\rangle$.

The $F(X)$ generated by q1, q2 acted by F, will it convert q3, q4 to $F(00)$ when the CNOT gate operation is performed? Will $F^{-1}$ also act on q1, q2 when it acts on q3, q4 because of the entanglement, so that the $F(X)$ will be converted to $X$?

Personally, I guess that in the end the output result of A will be $F(X)$, and the output result of B will be $00$. But I'm not sure that I'm right about this.

Martin Vesely · Answer 1 · 2024-04-28T06:50:12.893

Disclaimer: analysis below works only for gates $F$ changing phase only. Once absolute values of amplitudes are changed, other results than predicted below are returned.

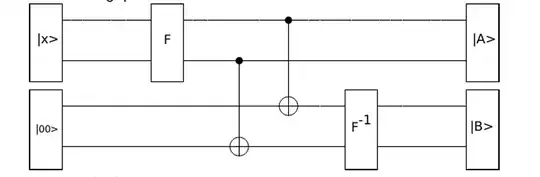
Lets analyze your circuit step by step. An initial state is $|x\rangle|00\rangle$. Then gate $F$ is applied and we are in state $|Fx\rangle|00\rangle$.

Next, two CNOTs work as so-called fan-out. This means that they copy state of first qubit to third one and state of second one to fourth one. Note however, that these copies are not idependent (i.e. once first qubit is changed, thrid one changes as well, similarly for pair of second and fourth qubits). This is consequence of no-cloning theorem (see more on fan-out and no-cloning theorem in this thread).

So, the fan-out switches our quatum computer to state $|Fx\rangle |Fx\rangle$. Still bear in mind that these "copies" are not independent! Application of gate $F^{-1}$ on third and fourth qubits changes them back to state $|x\rangle$. Because of dependency of the copies, this also happen on qubits no. 1 and 2. This means that $|A\rangle = |x\rangle$ and $|B\rangle = |x\rangle$.

However, these registers are entangled, i.e. changing pair of qubits 1 and 2 leads to same change in qubits 3 and 4, and vice versa.

You can try to play with this circuit in IBM Quantum composer:

OPENQASM 2.0;
include "qelib1.inc";
qreg q[4];
creg c[4];
ry(pi / 8) q[1];
rx(pi / 4) q[0];
barrier q[1];
barrier q[0];
cu1(pi/3) q[0], q[1];
barrier q[1];
barrier q[0];
cx q[0], q[2] ;
cx q[1], q[3];
cu1(-pi/3) q[2], q[3];

Once you comment gates cu1(pi/3) q[0], q[1]; and cu1(-pi/3) q[2], q[3]; you will see that both pairs of qubits are entangled, i.e. only states $|0000\rangle$, $|0101\rangle$, $|1010\rangle$ and $|1111\rangle$ are possible (with some amplitudes). This is compatible with fact that for pair of qubits there are four basis states and you nicelly see that both pairs of qubits are not independent. Now, uncomment gate cu1(pi/3) q[0], q[1];. Amplitudes are changed. Then uncomment the inversion cu1(-pi/3) q[2], q[3]; and you will see that amplitudes are the same as in case both gates were commented.

So, the circuit just prepares two entangled "copies" of two-qubit state $|x\rangle$, idependently of gate $F$ provided the gate $F$ changes only phase and not absolute value of probability amplitudes.

The reason why this works for phase changing gates is phenomenon known as phase kickback.

How to analyse a quantum circuit with an uncertain gate F?

1 Answers1