I think I understand well how the eigenvalue algorithm works but when I try to define it mathematically I have problems. Specifically I have the matrix U:
$$ U = \begin{pmatrix} 0 & i \\ i & 0 \end{pmatrix}\,. $$
And I set up the circuit as follows:
The circuit works but I can't demonstrate correct operation step by step.
I have to demonstrate that the circuit is able to approximate the value of the eigenvalues $i$ and $-i$ of the controlled-$U$ operator.
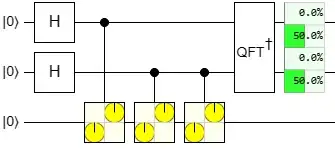
Calculate the wavefunction step by step by applying each gate in sequence $$ \begin{align} |000\rangle&\xrightarrow{H\otimes H}\frac12\sum_{a,b=0}^1|a\rangle|b\rangle|0\rangle\tag1\\ &\xrightarrow{CU}\frac12\sum_{a,b=0}^1i^a|a\rangle|b\rangle|a\rangle\tag2\\ &\xrightarrow{CU}\frac12\sum_{a,b=0}^1i^{a+b}|a\rangle|b\rangle|a\oplus b\rangle\tag3\\ &\xrightarrow{CU}\frac12\sum_{a,b=0}^1i^{a+2b}|a\rangle|b\rangle|a\rangle\tag4\\ &\xrightarrow{QFT^\dagger}\frac14\sum_{a,b=0}^1i^{a+2b}\sum_{x,y=0}^1i^{-(a+2b)(x+2y)}|x\rangle|y\rangle|a\rangle\tag5\\ &=\frac14\sum_{x,y=0}^1\sum_{a,b=0}^1i^{-(a+2b)(x+2y-1)}|x\rangle|y\rangle|a\rangle\tag6\\ &=\frac14\sum_{a,x,y=0}^1i^{-a(x+2y-1)}\left(\sum_{b=0}^1(-1)^{b(x+2y-1)}\right)|x\rangle|y\rangle|a\rangle\tag7\\ &=\frac14\sum_{a,x,y=0}^1i^{-a(x+2y-1)}\left(1-(-1)^{x+2y}\right)|x\rangle|y\rangle|a\rangle\tag8\\ &=\frac12\sum_{a=0}^1\left[|1\rangle|0\rangle+(-1)^a|1\rangle|1\rangle\right]|a\rangle\tag9\\ &=\frac{1}{\sqrt2}(|1\rangle|0\rangle|+\rangle+|1\rangle|1\rangle|-\rangle)\tag{10} \end{align} $$ The first qubit is the least significant qubit of the first register, so the final expression implies 50% probability of measuring $.01$ (encoding eigenvalue $i$) and $.11$ (encoding eigenvalue $-i$), as expected, c.f. this answer. Note that if the first register is measured, then the second collapses to the eigenvector corresponding to the eigenvalue read out from the first.