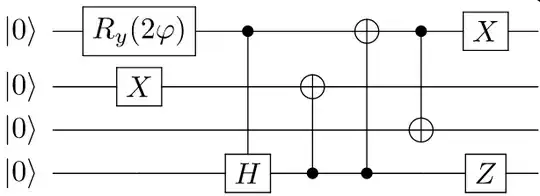
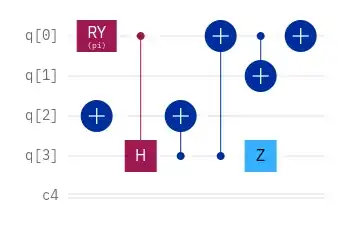
I need to rewrite a following circuit from Cirq to Qiskit with $2\varphi = \pi$.
It's a circuit representing an initial state for VQE calculation. Considering, that qiskit_nature considers a different ordering of spin-orbitals (first all spin-up, then all spin-down), I've rewritten the circuit like this (switching 1st and 2nd qubit, indexing from 0):
In both cases the statevector equals to
array([ 0. , -0. , 0. , -0. , 0. ,
-0. , 0.70710678, -0. , 0. , -0.70710678,
0. , -0. , 0. , -0. , 0. ,
-0. ])
, i.e.
$$ \left|\psi\right> = \frac{1}{\sqrt{2}}\left| 0110 \right> - \frac{1}{\sqrt{2}}\left| 1001 \right>. $$
In Cirq, the total angular momentum $\left<\psi \middle| S^2 \middle| \psi \right> = 0$, i.e. the state should be singlet. But when I try the same in qiskit with the help of second_q_ops(), I'm getting 1.999999....
Why does my result differ?
My Code
#!/usr/bin/env python3
import numpy as np
import qiskit_nature
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.providers.aer import Aer
from qiskit.quantum_info import Statevector
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.drivers import Molecule
from qiskit_nature.drivers.second_quantization import ElectronicStructureMoleculeDriver, ElectronicStructureDriverType
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.transformers.second_quantization.electronic import ActiveSpaceTransformer
if name == 'main':
qiskit_nature.settings.dict_aux_operators = True
backend = Aer.get_backend('statevector_simulator')
geometry = [('N', [0.000000000000, 0.000000000000, 0.000000000000]),
('C', [0.000000000000, 0.000000000000, 1.498047000000]),
('H', [0.000000000000, -0.938765985000, 2.004775984000]),
('H', [0.000000000000, 0.938765985000, 2.004775984000]),
('H', [-0.744681452, -0.131307432, -0.634501434])]
# Obtaining ground state
driver = ElectronicStructureMoleculeDriver(Molecule(geometry),
basis="sto3g",
driver_type=ElectronicStructureDriverType.PSI4)
as_transformer = ActiveSpaceTransformer(num_electrons=2, num_molecular_orbitals=2)
es_problem = ElectronicStructureProblem(driver, transformers=[as_transformer])
converter = QubitConverter(JordanWignerMapper())
# Create circuit
qreg_q = QuantumRegister(4, 'q')
circuit = QuantumCircuit(qreg_q)
circuit.x(qreg_q[2])
circuit.ry(np.pi, qreg_q[0])
circuit.ch(qreg_q[0], qreg_q[3])
circuit.cx(qreg_q[3], qreg_q[2])
circuit.cx(qreg_q[3], qreg_q[0])
circuit.cx(qreg_q[0], qreg_q[1])
circuit.z(qreg_q[3])
circuit.x(qreg_q[0])
print(f'Circuit:\n{circuit}')
statevec = Statevector(circuit).data
print(f'Statevector:\n{statevec}')
# Obtain S^2 operator
ss_op = es_problem.second_q_ops()['AngularMomentum']
print(f'S^2 operator:\n{ss_op}')
print(f'<psi|S^2|psi> = {statevec @ converter.convert(ss_op).to_matrix() @ statevec}')
The Output
Circuit:
┌───────┐ ┌───┐ ┌───┐
q_0: ┤ Ry(π) ├──■───────┤ X ├──■──┤ X ├
└───────┘ │ └─┬─┘┌─┴─┐└───┘
q_1: ───────────┼─────────┼──┤ X ├─────
┌───┐ │ ┌───┐ │ └───┘
q_2: ──┤ X ├────┼──┤ X ├──┼────────────
└───┘ ┌─┴─┐└─┬─┘ │ ┌───┐
q_3: ─────────┤ H ├──■────■──┤ Z ├─────
└───┘ └───┘
Statevector:
[ 0.00000000e+00+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
0.00000000e+00+0.j 0.00000000e+00+0.j 6.12323400e-17+0.j
7.07106781e-01+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
-7.07106781e-01+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
0.00000000e+00+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
0.00000000e+00+0.j]
S^2 operator:
Fermionic Operator
register length=4, number terms=12
(0.75+0j) * ( +_0 -_0 )
+ (0.75+0j) * ( +_1 -_1 )
+ (0.75+0j) * ( +_2 -_2 )
+ (0.75+0j) * ( +_3 -_3 )
+ (0.5+0j) * ( +_0 -_0 +_1 -_1 )
+ (-1.5+0j) * ( +_0 -_0 +_2 -_2 )
+ (-0.5+0j) * ( +_0 -_0 + ...
<psi|S^2|psi> = (1.9999999999999996+0j)