Using machine learning to determine a good initial mapping for a quantum circuit

Question

I am trying to use a machine learning model to find a good initial mapping for a quantum circuit. I am trying to minimise the number of swap operations i.e. the number of CNOT gates. This is my methodology -

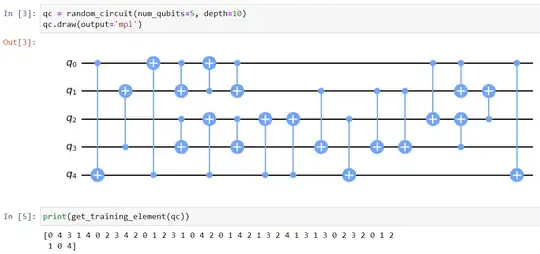
1. Generate a random quantum circuit with only CNOT gates. I generated a 5 qubit circuit and specified a random depth between 8 and 16 (No particular reason for picking these depths).

2. Extract the feature/x array for the quantum circuit by using the bits that each CNOT gate works on. For example, for the given circuit, the x array would look like this (Read in pairs) -

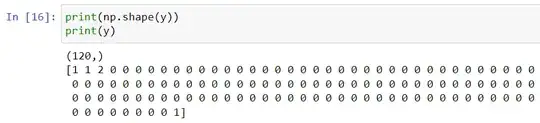
As a circuit with depth 5 will have lesser numbers than a circuit with depth 11, I padded all elements with 0s at the end with a maximum array length of 64. A few training elements would look like this -

3. Use the Qiskit transpiler to find the CNOT gate count of each possible initial mapping. As there are 5 qubits, there will be 5! = 120 different initial mappings possible. I then ran the qiskit.transpile function in a loop 120 times for each different initial mapping and found the CNOT gate count for each mapping using the transpiled_circuit.count_ops() function.

4. I thought of using a range of values as acceptable. So, anything between the minimum CNOT gate count and one standard deviation ahead of the minimum would be considered as acceptable. Among all the 120 different transpiled circuits with difference initial mappings, whichever layouts gave me a CNOT gate count within this range would be considered

5. Found all the acceptable layouts and encoded them in an array of size 120. For example, if layouts 0, 1, 2 and 119 were deemed to be acceptable, the encoded array would look like

6. The x array will be my training data and the encoded array will be my target data.

7. I repeated the above steps in a loop to generate a dataset of size 80000 i.e., eighty thousand random circuits of 5 qubits with a depth between 4 and 16 and their acceptable initial mappings as determined by the CNOT gate count by the Qiskit transpiler.

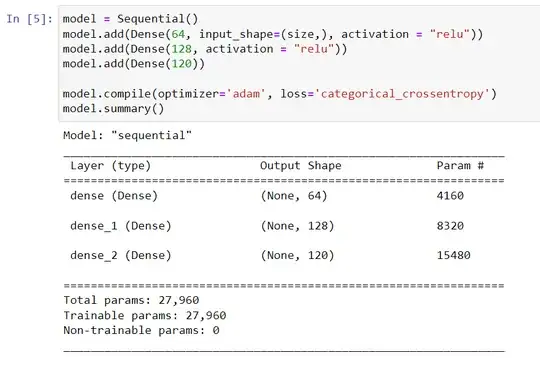
8. I normalise the x data and feed it to a dense neural network with the following architecture -

However, the network is not learning anything and the accuracy does not go above 1-2%. What am I doing wrong? Is this an error in my overall methodology or is this an error just in the ML model? Is there any way to fix this?

Answer 1

There are some serious issues in the choice of model architecture that will make learning almost impossible.

Below I'll comment on why this specific architecture and implementation is not going to work, but more generally I doubt that a vanilla feedforward NN is the right choice. I don't have experience with solving discrete problems with NN so I can't recommend anything with confidence, but graph neural networks might be promising. But whatever modifications you make, you should really focus on making the implicit relationships in your data explicit (see comments below).

---

For notation, let $\mathbf{x}\in[5]^{64}$ (with $[5]:=\{0,1,2,3,4\}$) be the model inputs, $\mathbf{y}\in \{0,1\}^{120}$ is the set of vector-valued patterns to predict, and $\hat{\mathbf{y}}$ is the output of the Neural Network (NN). I assume the "2" in the array of step 5 is meant to be a "1", i.e. $\mathbf{y}$ is a vector containing labels.

Here are some issues:

1. Your labels $\mathbf{y}$ are binary ("valid" versus "invalid") but you've used categorical_crossentropy loss. This loss function is for one-hot labels, which doesn't work for your application. Your choice of $\mathbf{y}$ is not really a label, so you need to find a more suitable loss function.

2. $\mathbf{x}$ is highly structured (e.g. sequential) but its being treated without any sort of inductive bias for the learning problem. There is a fundamentally different relationship between $x_0$ vs. $x_1$ compared to $x_0$ vs. $x_2$ but the weights in the input layer and subsequent layers are oblivious to this.

   • Recommendation: modify the architecture to account for the inherent structure represented in the elements of $\mathbf{x}$, e.g. using graph-valued inputs.

3. You're trying to learn a complicated discrete combinatorial problem using an approximator for functions with a continuous input domain (while your inputs are set to $[5]^{64}$, the domain of this NN is $\mathbb{R}^{64}$). If I recall, this kind of SWAP network problem in its general form is NP-hard. Worse, your network is very shallow and narrow - it is not expressive enough to learn anything close to a discrete function.

4. The structure of $\mathbf{y}$ - each element corresponding to a specific permutation of the values of elements of $\mathbf{x}$ - is also unknown to the NN. The NN would have to somehow learn an association between $\mathbf{x}$ and each element of $\mathbf{y}$ as being the result of a permutation on a graph. Not accounting for this kind of structure makes your NN's already hard task even more difficult.

   • Recommendation: Make the combinatorial relationship between $\mathbf{x}$ and $\mathbf{y}$ explicit. For example, "flatten" your inputs so that each $\mathbf{x}$ is associated with $5!$ distinct inputs to the NN, each with a single "0" or "1" as a label.