In introductions to superconducting qubits, we often take the classical LC circuit and then quantize the operators. Why are we allowed to do this?
I do not see this derivation anywhere -- what convinces us that the many electrons in a superconducting circuit will behave as a dynamical two-level system. It often says that the only dynamics in the superconducting circuit are the charge and flux oscillating but how do we know this?
The idea is to realise that classical physics is a limiting case of quantum physics. The limits (usually) are:
There are various other ways to think about it, but these are sufficient.
Now, the case of a transmon circuit being a quantum system comes from the low temperatures at which it is operated $(\approx 100 mK)$.
The energy level diagram of a transmon looks like this:
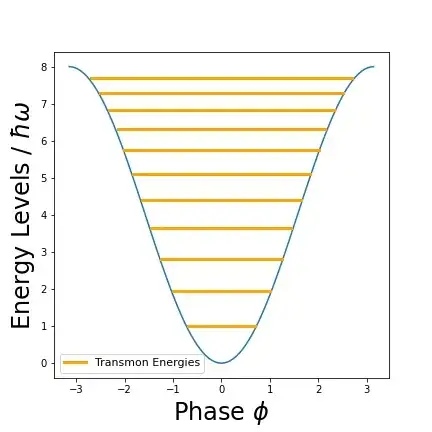
Now, as the energy $(E \propto kT)$ increases, the energy levels become too close by that they form an effective continuum. Thus as the energy/DoF increases, the system becomes closer to classical physics. There are no discrete energy levels in the continuum spectrum, and thus the 'quantum' nature of the circuit subsides. These ideas also apply to other quantum systems in general. You may refer to concepts such as the equipartition theorem to better understand how energy and DoF are related.
A simple way to understand this idea in terms of some numbers, at room temperature $(300 K)$, the thermal energy is $\approx 26 meV$ whereas the qubit energy of is $\approx 3 \mu eV$. Thus, all the low lying energy states are filled at room temperature and can't be used to process quantum information. (A qubit in the ground state can spontaneously excite to a higher level by absorbing energy from the environment)
On the other hand, at about $T = 30 mK$, the thermal energy is comparable to the qubit energy.
