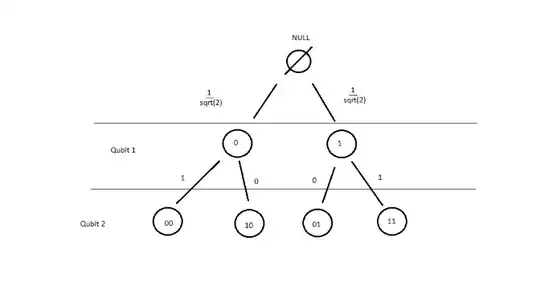
I've been learning about quantum computing, and I noticed that another way to describe the state vector is as a path in a binary tree where each level of tree represents another qubit, each node represents a state, and the edge weights represent the probability amplitude of moving from one state to another. Here's an example: (Sorry for MS Paint!)
Now what's interesting is that if you start with a state vector of |0>, placing qubits into superposition opens paths in the tree, while entanglement and "measurement" close paths. I was working this out with the sudoku example in the qiskit textbook at Qiskit Grover's Algorithm Example, and I found that if you adhere to the following principles, you can find the solution state while avoiding false paths in the tree just by following the quantum circuit:
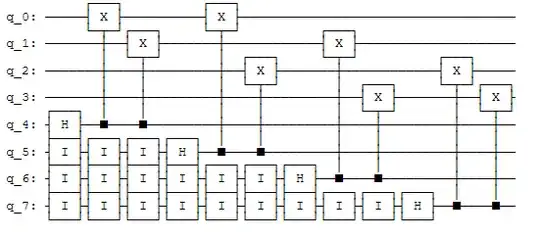
- Start with a linear tree with every bit in the 0 state.
- Place a single variable qubit into superposition, creating a single sub-tree/branch.
- Apply all CNOT gates related to that qubit to close off any potential branching and adjust the states of the nodes appropriately.
- Whenever a "clause bit" (as described in the link above) no longer has any more gates attached to it, or is no longer being interacted with, close all branches where the nodes do not have the "clause bit" in a position of 1.
- Place the next variable qubit into superposition and repeat 3 & 4, until all variable qubits have been placed into superposition.
So, the circuit design would look like this (forget about the diffuser and toffoli for the moment):
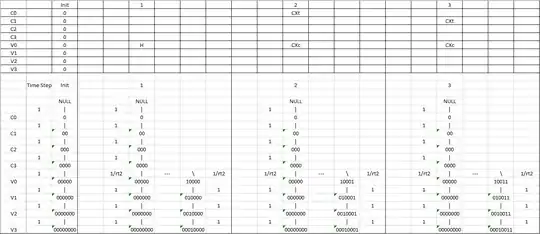
I did a step-by-step implementation of this in excel, drawing out all of the trees, and I found that only two main sub-trees form (one for each solution) and that at most only four sub-trees/branches are present at any one time. Furthermore, at the end, all of the clause bits were in the state 1. Now considering that there are a total of 8 qubits in this system, a total of 256 different paths are possible. Is this just a trivial example or could this actually be implemented as a viable algorithm for path finding?
Edit: P.S. Could this answer P = NP? Also I noticed my quantum circuit isn't quite correct.