Let $P \in \mathbb{R}^2$ and define
$$ d(x,y) = \left\{ \begin{array}{lr} ||x-y|| & \text{if} \; \; x,y,P \; \; \text{are collinear,}\\ || x - P|| + ||y-P||& \;\;\;\; \text{otherwise.} \end{array} \right. $$
How can I show this metric satisfies the triangle inequality? I am trying to visualize how the open balls look but I cannot see to find out.
In German it is called the french railway metric . The reason for this is that in the earlier France, the distance to get from one city to the other by train was the same as getting to Paris and then to the target city (the railway system being centralized in Paris). This explanation also yields the intuition for your metric. (Also called the British Rail metric by substituting Paris with London)
The proof is as easy as it gets: On every line through $P$ it is clearly a distance. Then go through each case whether you have two points on a line through $P$ and one not or three points which are not on any common line through $P$. Keep in mind the intuition from above and you will get there (you essentially do nothing but saying: to go from one city over Paris to another city over Paris to a third city is longer than going from one city over Paris to another - this amounts to the triangle inequality) (so another hint to express this in mathematical language: $d(x,y) = d(x,P) + d(P,y)$ (i.e. go from $x$ to $x$ over $P$) and now use triangle inequalities for each summand i.e. triangle inequalities for the triples $x,P,z$ and $z,P,y$ and see what happens).
If you would like me to give a detailed solution, I will be happy to do that. But I think I gave you some good hints, which will lead you to the solution, and you will learn a lot from this, hence the shortness.
Cheers
(By request of the OP.)
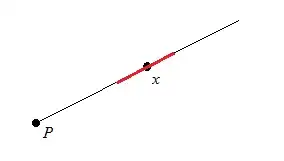
If $x$ is a point different from $P$, and $\epsilon\le\|x-P\|$, the $\epsilon$-ball centred at $x$ is an open interval of length $2\epsilon$ centred at $x$ on the line $\overline{Px}$:
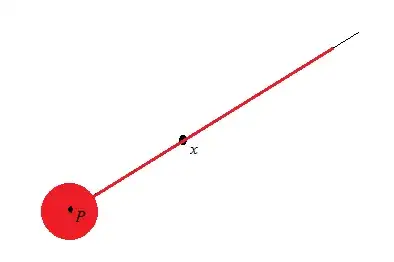
If $\epsilon>\|x-P\|$, the $\epsilon$-ball at $x$ consists of the segment $\overline{Px}$, the open ray of length $\epsilon$ extending from $x$ away from $P$ on the line $\overline{Px}$, and the ordinary open ball of radius $\epsilon-\|x-P\|$ centred at $P$:
In other words, in every case it contains all of the points that are less than $\epsilon$ away from $x$ provided that you can move only along lines passing through $P$. You must always be moving directly towards or directly away from $P$.
Finally, the $\epsilon$-ball at $P$ is just the ordinary Euclidean $\epsilon$-ball at $P$.
For the triangle inequality, let $x,y$, and $z$ be any three points; we wish to show that $$d(x,y)\le d(x,z)+d(z,y)\;.$$
Consider first the case in which $x,y$, and $P$ are collinear. If $z$ is also on this line, $d$ reduces to the usual Euclidean metric, so assume that this is not the case. Then $d(x,z)=\|x-P\|+\|P-z\|$, $d(z,y)=\|z-P\|+\|P-y\|$, and $d(x,y)\le\|x-P\|+\|P-y\|$ by the triangle inequality for the Euclidean metric, so
$$\begin{align*} d(x,y)&\le\|x-P\|+\|P-y\|\\ &\le\big(\|x-P\|+\|P-z\|\big)+\big(\|z-P\|+\|P-y\|\big)\\ &=d(x,z)+d(z,y)\;. \end{align*}$$
Now assume that $x,y$, and $P$ are not collinear, so that $d(x,y)=\|x-P\|+\|P-y\|$. If $z$ is not on either of the lines $\overline{Px}$ and $\overline{Py}$, then
$$\begin{align*} d(x,y)&=\|x-P\|+\|P-y\|\\ &<\big(\|x-P\|+\|P-z\|\big)+\big(\|z-P\|+\|P-y\|\big)\\ &=d(x,z)+d(z,y)\;. \end{align*}$$
If $z$ is on one of those lines, we may assume without loss of generality that it’s on $\overline{Px}$. Then $\|x-P\|\le\|x-z\|+\|z-P\|$ by the triangle inequality for the Euclidean metric, so
$$\begin{align*} d(x,y)&=\|x-P\|+\|P-y\|\\ &\le\big(\|x-z\|+\|z-P\|\big)+\|P-y\|\\ &=\|x-z\|+\big(\|z-P\|+\|P-y\|\big)\\ &=d(x,z)+d(z,y)\;. \end{align*}$$
