4

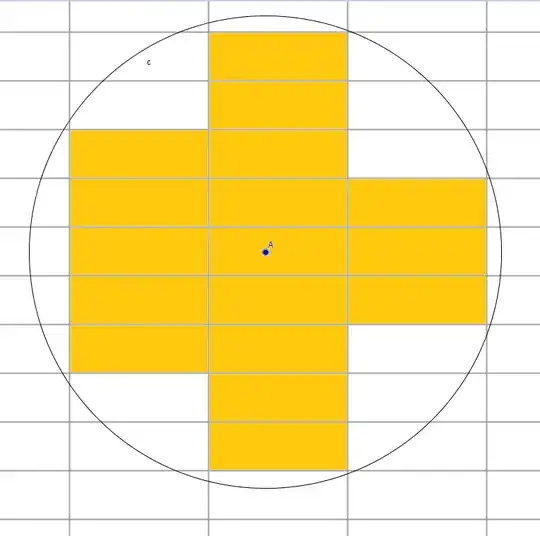
Let us construct a grid consisting of rectangles of height $h$ and width $w$. When we place a circle of radius $r$ over this grid, there is a certain amount of rectangles that completely lie within the circle.

When moving around the circle (note that this only has to happen on an interval $[0,w)\times[0,h)$ since we're looking at a grid), we will obtain a maximum number $N_\max$ of rectangles that fit into the circle.

Now the question arises: Is there always a placement of the circle possible such that the grid is symmetric in the two axes through the center of the circle which also has $N_\max$ rectangles inside of it?

Clarified: Assume we know $N_\max$. A figure consisting of $N_\max$ rectangles that fit inside our circle need not be symmetric in $x$ and $y$-direction. But can we find a figure consisting of the same amount $N_\max$ that is symmetric in $x$ and $y$-direction and fits in our circle.

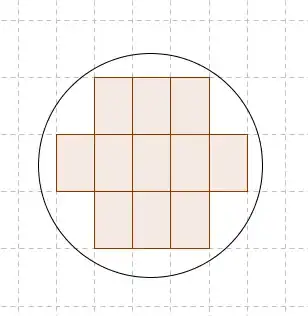
Here we see a symmetric solution with $N_\max=11$, but can we always find a symmetric solution?

Circle with rectangles in it

konewka
  • 1,612
  • Have a look at the best packing of 8 squares in a circle at http://www2.stetson.edu/~efriedma/squincir/ – Gerry Myerson Oct 14 '14 at 11:42
  • Of possible interest: http://stackoverflow.com/questions/3927380/maximum-packing-of-rectangles-in-a-circle – Gerry Myerson Oct 14 '14 at 11:44
  • @GerryMyerson, those solutions aren't aligned in a grid, so the packings of 1, 2, 4, 5, 12,... are usable in this problem, but I'm afraid the other ones aren't – konewka Oct 14 '14 at 11:58

1 Answers1

2

I have implemented an algorithm myself that counts the amount of rectangles ($w\times h$) inside a circle with radius $r$ with its centre at $(x,y)$.

I then took $(x,y)$ in the rectangle $[0,w]\times[0,h]$ and looked what their amount of rectangles was.

Making a contour plot of that gave me an insight in the behaviour of the amount of rectangles, which looks enormously interesting.

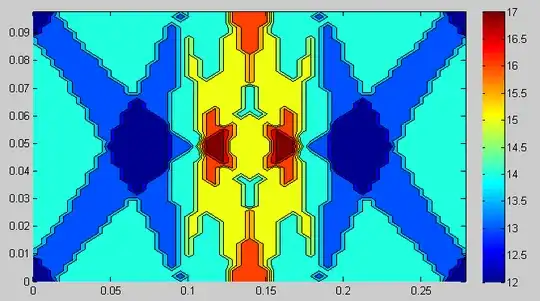
For a random $w=0.2785, h=0.0975, r=0.4728$, the result was: Contour plot of the amount of rectangles inside the circle

This has a maximum of 17, but it is located just off-centre, and we see the amount is only 16 at $(\frac{w}{2},0)$, so there is no symmetric solution for this specific $w,h,r$.

It should be noted that I had to try a few random values before finding a non-symmetric case, I can't yet explain why symmetry is so common.

Below one can find the circle in an optimal setup Circle of given <span class=$w,h,r$ above with 17 rectangles within them">

konewka
  • 1,612