How can a function have a vertical tangent and be continuous?

Question

I read somewhere that, "a function with a vertical tangent may be continuous but not differentiable."

Is this correct and, if so, what is an example of it?

I can't think how a function with an asymptote can be continuous.

Note "vertical tangent" and "asymptote" are different concepts. — David Mitra, Jan 07 '12 at 18:52
A closely related question: http://math.stackexchange.com/questions/35956/given-lim-limits-x-to-af-primex-infty-what-can-be-concluded-about-f — Jonas Meyer, Jan 07 '12 at 19:00
I now understand this @DavidMitra :) That's awesome! I feel like I just discovered a new creature! A function with a vertical tangent that is continuous and not differentiable! — Korgan Rivera, Jan 07 '12 at 19:24
Look at robojohn's picture. The graph has a vertical tangent at $x=0$. To me, a vertical asymptote at $x=a$ means that the function "blows up" at $a$; that is, the values of the function approach infinity (or negative infinity) as you approach $a$. — David Mitra, Jan 07 '12 at 19:26
@DavidMitra, I guess you posted that after I changed my comment :) — Korgan Rivera, Jan 07 '12 at 19:27

robjohn · Accepted Answer · 2012-01-08T00:16:09.593

15

Adding a graphic to yoyo's comment:

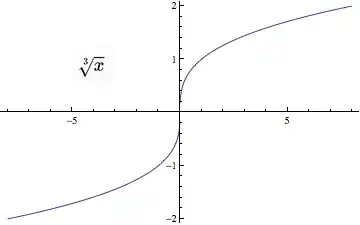
cube root plot

$\sqrt[3]{x}$ is continuous, but its derivative, $\dfrac{1}{3\sqrt[3]{x^2}}$, tends to $\infty$ near $0$.

edited Jan 08 '12 at 00:16

answered Jan 07 '12 at 19:22

robjohn

353,833

2

But note that having a vertical tangent is not the same as the derivative tending to $\infty$. Having a vertical tangent at $x_0$ means having for every $M>0$ a neighbourhood $U$ where $|\frac{f(x)-f(x_0)}{x-x_0}|>M$ for all $x\neq x_0$ in $U$ (anti-Lipschitz). Indeed $f$ need not be differentiable anywhere. The Weierstrass function appears to have vertical tangents, and if this is so, these are it's only tangents. – Marc van Leeuwen Jan 07 '12 at 20:25
1

Just curious: why $x^{1/3}$ instead of the simpler-looking $\sqrt{x}$? :-) – Srivatsan Jan 07 '12 at 22:59
2

@Srivatsan: $\sqrt[3]{x}$ is continuous on both sides of the vertical tangent and, to me, gives a better image of what is going on. Certainly, we could use $\sqrt{|x|}$, whose image with a cusp looks worse, or $\operatorname{sgn}(x)\sqrt{|x|}$, which is not "simpler-looking". In any case, is $x^{1/2}$ really that much simpler-looking than $x^{1/3}$? (Also, I was working from yoyo's comment.) – robjohn Jan 08 '12 at 00:06
@robjohn I hope you didn't miss the smiley at the end of my comment. =) I like your nicely phrased comment though. [I meant "simpler-looking" as an expression, not the graph. Yes, the graphs look pretty much the same to me.] – Srivatsan Jan 08 '12 at 00:11
x^1/3 is still differentiable, just not continuosly differentiable, i.e., the difference quotient limit (at 0) is well defined, as its limit exist on both sides, it just happens to be inifinity. Compare w/ |x| which is instead not differentiable, bc limits on both side differ. – Three Diag Jan 11 '16 at 13:13
1

@ThreeDiag: that depends on who you ask. Some people consider an infinite limit not to exist in this sense since infinity is not a real number. – robjohn Jan 11 '16 at 14:12

score 2 · Answer 2 · answered Jan 07 '12 at 18:54

2

The idea is just that even though the slope is vertical, you can still approach your point when getting close enough ; the fact that the slope is vertical doesn't mean your function goes to infinity. Among well-known examples, $f(x) = \alpha x^{1/n}$ with $n \ge 1$.

Hope that helps,

answered Jan 07 '12 at 18:54

Patrick Da Silva

42,548

You mean $n$ odd and greater than $1$? (and $\alpha\neq 0$) – Jonas Meyer Jan 07 '12 at 18:59
@JonasMeyer, or any $n>1$, with the domain of $f$ declared to be $[0,\infty)$. – hmakholm left over Monica Jan 07 '12 at 19:02
@Henning: Sure, or the odd extension of such a function to $\mathbb R$ (or even extension if cusps are allowed). – Jonas Meyer Jan 07 '12 at 19:04
@Jonas: or what I did to make the plot in my answer since Mathematica balks at x^(1/3) for $x<0$: $\operatorname{sgn}(x)|x|^{1/n}$. This works for all $n>1$. – robjohn Jan 07 '12 at 19:44
@robjohn: Yes, that is exactly the odd extension of $x^{1/n}$ from $[0,\infty)$ to $\mathbb R$, but it doesn't given an example when $n\leq 1$. – Jonas Meyer Jan 07 '12 at 19:46
@Jonas: okay, I wasn't sure, but it makes sense now. The $n>0$ was a typo. – robjohn Jan 07 '12 at 19:52
Man, downvoters these days you don't have it. – Patrick Da Silva Jan 09 '12 at 16:09

score 2 · Answer 3 · answered Jan 07 '12 at 21:45

As described above, $f(x) = x^{1/3}$ is continuous at $0$ and has a vertical tangent at $0$.

To understand this example more fully, it may be helpful to recall the epsilon-delta definition of "continuous at $0$".

Loosely paraphrased, "$f$ is continuous at $0$" means that for every $\epsilon>0$, we can find $\delta>0$ such that inputs within $\delta$ of $0$ will "force" the outputs to be within $\epsilon$ of $0$.

In the example of $f(x)=x^{1/3}$ at $x=0$, it is true that for every $\epsilon$ there exists a $\delta$. For example, if $\epsilon = 0.01$, we can choose $\delta = 0.000001$. Similar statements can be made for any $\epsilon>0$.

All that matters is that we can find a $\delta$ for every $\epsilon$. But $\delta$ is allowed to be much smaller than $\epsilon$. It might happen that $\delta$ is not a linear function of $\epsilon$, but instead approaches $0$ much "faster" than $\epsilon$ does.

How can a function have a vertical tangent and be continuous?

3 Answers3

Linked