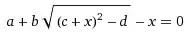Maxima can't solve relatively simple equation.

Question

I'm trying to solve this equation for x, with Maxima:

What I am doing wrong here?

declare([a, b, c, d], constant);
solve(a+b*sqrt((c+x)^2 - d) - x);

[x=b*sqrt(x^2+2*c*x-d+c^2)+a]

Obviously that is not a solution - x is on both sides!

Wolfram alpha solves it no problem:

Is Mathematica just much better than Maxima?

Answer 1

This method is to complicated. Five lines are sufficient. Check the first lines of this answer. I will repair this later.

It seems that Maxima isn't able to do this without assistance.

I use the method that is shown in this answer by @BillDubuque.

We use the variable w in our calculation and want to be sure that it has not assigned any value.

(%i1) kill(w)
(%o2)                                done

We define the equation we want to solve:

(%i2) eq1:a+b*sqrt((c+x)^2-d)-x
                                       2
(%o2)                    b sqrt((x + c)  - d) - x + a

The global variable algebraic must be set to true in order for the simplification of algebraic integers that we define with tellrat to take effect.

(%i3) algebraic:true
(%o3)                                true

The we need the expression under the square root for the tellrat and the subst statement. One can copy and paste it or type it in but I use a Maxima function to extract this part from the equation.

(%i4) t1:part(eq1,1,2,1)
                                        2
(%o4)                            (x + c)  - d
(%i5) tellrat(w^2 = t1)
                             2             2        2
(%o5)                   [(- x ) - 2 c x + w  + d - c ]
(%i6) subst(w^2,t1,eq1)
(%o6)                        (- x) + b abs(w) + a

The % references the result of the previous statement.

(%i7) solve(%,w)
                                          a - x
(%o7)                         [abs(w) = - -----]
                                            b
(%i8) %^2
                                             2
                                  2   (a - x)
(%o8)                           [w  = --------]
                                          2
                                         b

The function rattriggers the reductions defined in tellrat.

(%i9) rat(%)
                                            2            2
                      2                2   x  - 2 a x + a
(%o9)/R/            [x  + 2 c x - d + c  = ---------------]
                                                  2
                                                 b
(%i10) solve(%,x)
                       2           2            2     2
              b sqrt((b  - 1) d + c  + 2 a c + a ) + b  c + a
(%o10) [x = - -----------------------------------------------,
                                   2
                                  b  - 1
                                        2           2            2     2
                               b sqrt((b  - 1) d + c  + 2 a c + a ) - b  c - a
                           x = -----------------------------------------------]
                                                    2
                                                   b  - 1

This is the result we want.

We can combine the last few commands into one command to make the code more compact. I prefer the way were we can see the intermediate results

(%i11) solve(rat(solve(subst(w^2,t1,eq1),w)^2),x)
                       2           2            2     2
              b sqrt((b  - 1) d + c  + 2 a c + a ) + b  c + a
(%o11) [x = - -----------------------------------------------,
                                   2
                                  b  - 1
                                        2           2            2     2
                               b sqrt((b  - 1) d + c  + 2 a c + a ) - b  c - a
                           x = -----------------------------------------------]
                                                    2
                                                   b  - 1

Now we can reset the resources that we need only temporary to avoid unexpected side effects in later computations.

(%i12) kill(t1)
(%o12)                               done
(%i13) untellrat(w)
(%o13)                                []

Answer 2

I get as answer, I have added some white space, with GNU Maxima 5.32.1

%union(
%if(?%and(
-%pi/2 < parg(
    -(b*(c+a)-sqrt(b^2*d-d+c^2+2*a*c+a^2))/(b^2-1)
),
parg(
    -(b*(c+a)-sqrt(b^2*d-d+c^2+2*a*c+a^2))/(b^2-1)
) <= %pi/2),
[x = -(-b*sqrt(b^2*d-d+c^2+2*a*c+a^2)+b^2*c+a)/(b^2-1)],%union()),
%if(?%and(
-%pi/2 < parg(
    -(sqrt(b^2*d-d+c^2+2*a*c+a^2)+b*(c+a))/(b^2-1)
),
parg(
    -(sqrt(b^2*d-d+c^2+2*a*c+a^2)+b*(c+a))/(b^2-1)
) <= %pi/2),
[x = -(b*sqrt(b^2*d-d+c^2+2*a*c+a^2)+b^2*c+a)/(b^2-1)],%union()))

The maxima code was

display2d : false;
load("to_poly_solve");
eq : a+b*sqrt((c+x)^2-d)-x;
%solve([eq],[x]);