0

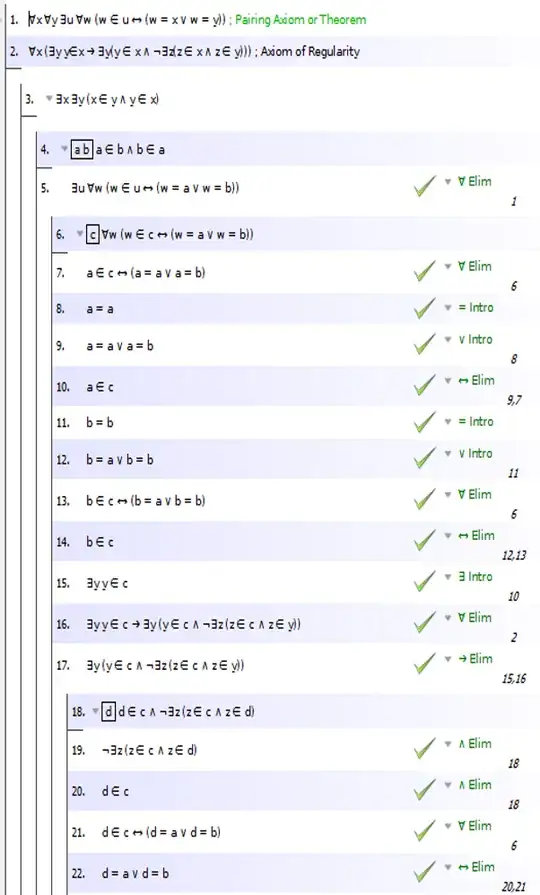
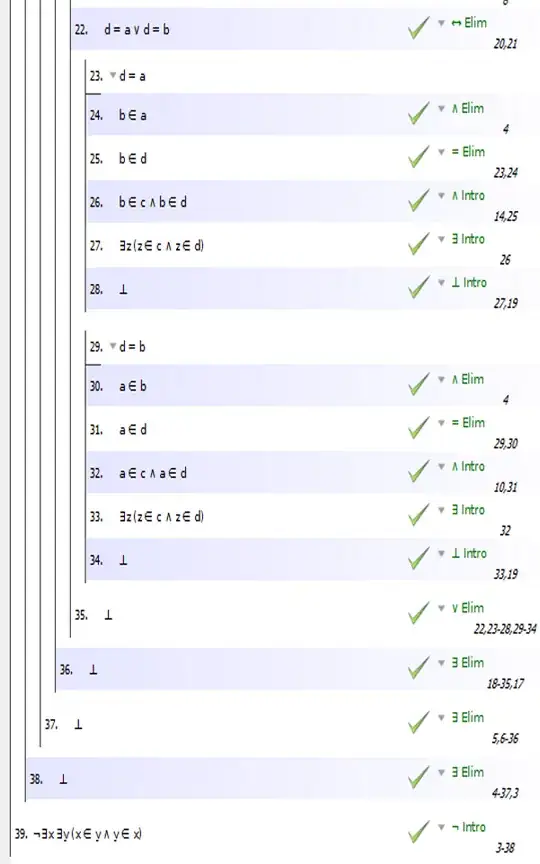
From the ZFC axiom of regularity, which states that every non-empty set contains an element disjoint from it, we can deduce that there is no set $A$ such that $A \in A$.

A proof is outlined here:

Let $A$ be any set. Then $\{A\}$ is a set, and by regularity $\{A\}$ must contain an element disjoint from $\{A\}$. The only element of $\{A\}$ is $A$, so $A\cap\{A\}=\varnothing$, and it follows immediately that $A\notin A$.

I am trying to convince myself that there cannot exist distinct sets $A$ and $B$ such that $B \in A$ and $A \in B$ using the same axiom, but I am no expert in logic and wonder whether this is true, and how this can be deduced.

The main issue I see is we end with infinite recursion. Suppose $A = \{B,C\}$ and $B=\{A,D\} = \{ \{B,C\}, D \}$.

Do we arrive at a contradiction somehow, and is $B$ considered a member of $B$?

Khashayar Baghizadeh
  • 1,531
jII
  • 3,158

3 Answers3

2

Here is a formal proof in Fitch:

enter image description here

enter image description here

Bram28
  • 103,721
1

Yes, it's true. Apply the axiom of regularity to the set $\{A, B\}$.

You ask whether you can prove $B \in B$. Of course, this is not a meaningful question with the axiom of regularity, since your premise is false. However, without the axiom, I believe the relations $B \in A \in B$ do not imply that $B \in B$.

user180040
  • 468
1

So I think the issue is a matter of perspective. The infinite recursion that you see is actually the contradiction. The Axiom of Regularity says that your construction is against the rules.

Axioms are rule of set theory that dictates how one must define a set. Therefore your idea of 'infinite recursive' is simply a violation of the rules, or axioms, of set theory.

Certainly there could be alternative axioms that incorporate your point of view but part of learning to use $ZFC$ and axioms is realizing that you are ultimately restricted to the basic assumptions: axioms.

tmastny
  • 488