I need to use it in a small step in the middle of a simulation and I think I'm not getting correct results to this probabilities and so for my all subsequent simulation. Could someone please check my results and my proof below?
I would like to obtain the law of the first hitting time of a geometric Brownian motion.
More precisely, to compute $\mathbb P [\tau_B \leq T]$ where $$\tau_B := \inf\{0 \leq t \leq T: X_t \leq B \}$$
and $X = (X_t)_{t \geq 0}$ is a geometric brownian motion of drift $\mu$ and volatility $\sigma$ with initial condition $X_0> B$.
It's known that it can be obtained in terms of the law of the minimum/maximum of a drifted Brownian motion.
Indeed, since $X_t = X_0 \exp ((\mu -\frac{\sigma^2}{2})t + \sigma W_t )$ and $\{\tau_B\leq T\}= \{X_T^*\geq B\}$ where $X^* = (X_t^*)_{t \geq 0}$ defined by $X^*_t =\min_{t \in [0,T]} X_t$, one can write
\begin{align} \mathbb P [\tau_B \leq T]&= \mathbb P [X_T^*\leq B]\\ &= \mathbb P \left[\xi_T^{(\lambda)}\leq \ln \left(\frac{B}{X_0}\right)\right] \end{align}
where $\xi_t^{(\lambda)}=\min_{s \in [0,t] }\{\bar{\mu} t+\sigma W_t \}= \min_{s \in [0,t] }\{\lambda t + W_t \}$ (last equality comes by scaling) with $\bar{\mu}=(\mu -\frac{\sigma^2}{2}) $ and $\lambda=\frac{\bar{\mu}}{\sigma^2}$.
Then one can just use the formula (see here for reference, the proof is a straightforward application of Girsanov theorem)
$$\mathbb P \left[\Lambda_T^{(\eta)}\geq x\right]=e^{2\eta x}\mathcal N\left(\frac{-x-\eta t}{\sqrt t}\right)+\mathcal N\left(\frac{-x+\eta t}{\sqrt t}\right)$$
for the law of the maximum of the drifted Brownian motion $\Lambda_t^{(\eta)} := \max_{s \in [0,t] }\{\eta t+W_t \}$. Therefore since by symmetry $\Lambda_t^{(\eta)}\overset{\mathcal L} {=} -\xi_t^{(-\eta)}$ where $\xi_t^{(\eta)} :=\min_{s \in [0,t] }\{-\eta t+ W_t \}$ is the minimum of the drifted brownian motion, one can can obtain the following formula
\begin{align} \mathbb P [\tau_B \leq T]&= \mathbb P [X_T^*\leq B]\\ &= \mathbb P \left[\xi_T^{(\lambda)}\leq \ln \left(\frac{B}{X_0}\right) \right] \\ &= \mathbb P \left[-\Lambda_T^{(-\lambda)}\leq \ln \left(\frac{B}{X_0}\right) \right] \\ &=e^{2\lambda \ln \left(\frac{B}{X_0}\right)}\mathcal N\left(\frac{ \ln \left(\frac{B}{X_0}\right)+\sigma^2 \lambda T}{\sigma \sqrt T}\right)+\mathcal N\left(\frac{ \ln \left(\frac{B}{X_0}\right)-\sigma^2 \lambda T}{\sigma \sqrt T}\right)\\ &=\left(\frac{B}{X_0}\right)^{2\lambda}\mathcal N\left(\frac{ \ln \left(\frac{B}{X_0}\right)+\bar{\mu} T}{\sigma \sqrt T}\right)+\mathcal N\left(\frac{ \ln \left(\frac{B}{X_0}\right)-\bar{\mu} T}{\sigma \sqrt T}\right) \end{align}
Please let me know if you notice any mistake.
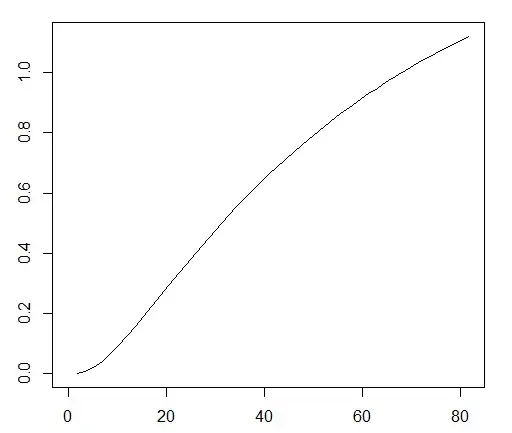
I'm having values bigger than one and an unexpected shape for the function $f(B) := \mathbb P [\tau_B \leq T]$ as you can see below in the graphic (Axes $y =f(B)$ and $x =B$; here X_0= 68).
I forced it to be 1 for barrier values equal or higher than the initial value. Nonetheless I think there is still a problem with the formula not only it should be automatically 1 for $B \leq X_0$. The probabilities I have calculating it by Monte Carlo are higher than the values obtained by this formula as you can see in the second graphic bellow.
Many thanks