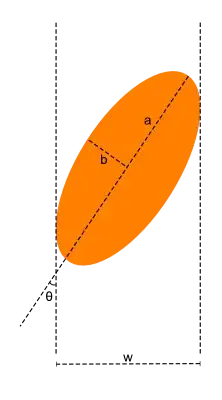
The unrotated ellipse can be parametrized as
$$\begin{pmatrix}a\cos\varphi\\b\sin\varphi\end{pmatrix}$$
so the rotated form (given the fact that you are apparently measuring rotation angle against vertical instead of horizontal and clockwise instead of counter-clockwise) would be
$$\begin{pmatrix}
\sin\theta & -\cos\theta \\
\cos\theta & \sin\theta
\end{pmatrix}
\begin{pmatrix}a\cos\varphi\\b\sin\varphi\end{pmatrix}
$$
The $x$ coordinate of that is
$$x=a\cos\varphi\sin\theta - b\sin\varphi\cos\theta$$
To look for extremal values in $x$ direction, compute the derivative:
$$\frac{\mathrm dx}{\mathrm d\varphi} =
-a\sin\varphi\sin\theta-b\cos\varphi\cos\theta\overset!=0\tag1$$
Take this equaton together with a second equation to express your width. All my ellipses so far are centered around the origin, so the maximal $x$ coordinate is at distance $\frac w2$ from the vertical axis, which leads to the second equation
$$x=a\cos\varphi\sin\theta - b\sin\varphi\cos\theta\overset!=\frac w2\tag2$$
Now you can combine these two equations to eliminate $\varphi$. I did so using resultants. The result is a single equation
$$w^2=(2a\sin\theta)^2+(2b\cos\theta)^2\tag3$$
Actually the resultants offer a second possible solution, namely $(a\sin\theta)^2+(b\cos\theta)^2=0$, but that's a degenerate situation where at least one of your semi-axes has length zero.
I coudln't yet make Wolfram Alpha do the variable elimination. In case you are interested in the Sage code behind my computation, here it is:
sage: R1.<t, sintheta, costheta, a, b, w> = QQ[]
sage: cosphi = (1-t^2)/(1+t^2) # rational parametrization
sage: sinphi = (2*t)/(1+t^2)
sage: v1 = vector([a*cosphi, b*sinphi])
sage: rottheta = matrix([
....: [sintheta,-costheta],
....: [costheta,sintheta]])
sage: v2 = rottheta*v1
sage: c1 = v2[0].derivative(t)
sage: c2 = v2[0] - w/2
sage: c3 = c1.numerator().resultant(c2.numerator(), t)
sage: c3.factor()
(4) * (-4*sintheta^2*a^2 - 4*costheta^2*b^2 + w^2) * (sintheta^2*a^2 + costheta^2*b^2)