$\mathbf{Revised\,3}$ (to reflect the OP's concern)
And all the above/previous $\mathbf{erased}$ with much gusto, after recognising that any geometric proof of it will likely be circular, so it will lead one to endless circles... (probably because of the symmetry of the particular congruence).
I think, but I am not sure, that it can be solved another way. If we can prove that the quadrilateral $DFEA$ is inscribable, then one may try using the corresponding ratios one gets from the power of the points $B$ and $C$ relative to the circumscribed circle of that quadrilateral. Perhaps the assumptions are enough to make those powers equal, hence all the goodies therein.
$\mathbf{Addendum\,\,2}$
And indeed, it looks like Desargues' with the additional assumptions $AD=AE$ and $BF=FC$, which should be immediate.
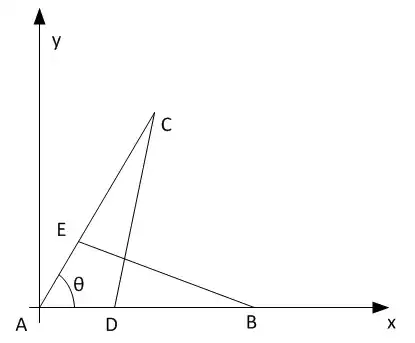
Sketch of proof for the general case:
- Construct circumcircle $c$ of isosceles $ADE$.
- Select point $B$ on the extension of $AD$.
- Conduct $BE$. It will intersect circumcircle $c$ at $F$.
- Conduct $DF$. It will intersect $AE$ at $C$ (see [*]).
- Now apply Desargues (powers of points $B$ and $C$ relative to the circumscribed $c$), using the additional assumptions $AD=AE$ and $BD=FC$.
- Under the two assumptions, 5) implies $F$ lies on the bisector of $A$, and everything else follows.
[*] The degenerate case of the above construction, is when $DE$ is a diameter of $c$. In this case the inscribed quadrilateral will be a square, with both its diagonals diameters, but in this case assumptions $BF=FC$ don't make sense, so this case is rejected. If you omit this case, point $C$ exists.
Needs a lot of work to see fully. If you don't see it, I will try to add more to this.