Say you have this type of cubic Bézier curve:
The 4 control points A,B,C,D have restrictions:
A & B have the same Y-axis coordinate
C & D have the same Y-axis coordinate
B & C have the same x-axis coordinate
My question is:
How do you express the X-axis coordinate of the inflection point of the red curve in function of the control points?
It is a bit related to this question, but the restrictions of the control points are an issue for me..
Thanks.
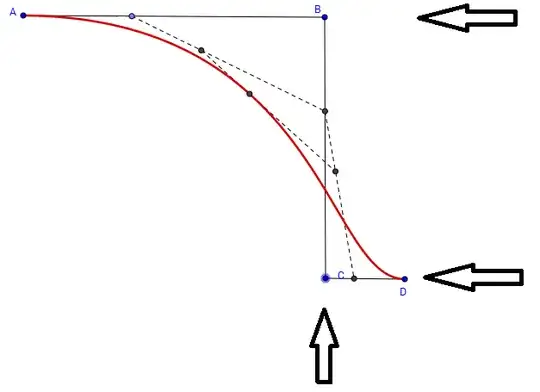
Without loss of generality you can choose your coordinate system such that
\begin{align*} A&=\begin{pmatrix}0\\1\end{pmatrix} & B&=\begin{pmatrix}x\\1\end{pmatrix} & C&=\begin{pmatrix}x\\0\end{pmatrix} & D&=\begin{pmatrix}1\\0\end{pmatrix} \end{align*}
Then the Bézier curve is
$$ P(t) = \begin{pmatrix} 3t(1-t)x + t^3 \\ (2t+1)(1-t)^2 \end{pmatrix} = \begin{pmatrix}t^3 - 3t^2x + 3tx \\ 2t^3 - 3t^2 + 1\end{pmatrix} $$
Now if you differentiate, you get
\begin{align*} P'(t) &= (3t^2 - 6tx + 3x, 6t^2 - 6t) \\ P''(t) &= (6t - 6x, 12t - 6) \end{align*}
Looking for the point where they both point in the same direction, you compute the determinant of these two vectors:
$$ \begin{vmatrix} 3t^2 - 6tx + 3x & 6t - 6x \\ 6t^2 - 6t & 12t - 6 \end{vmatrix} =-18\cdot\bigl((2x - 1)t^2 - 2xt + x\bigr) \overset!=0 $$
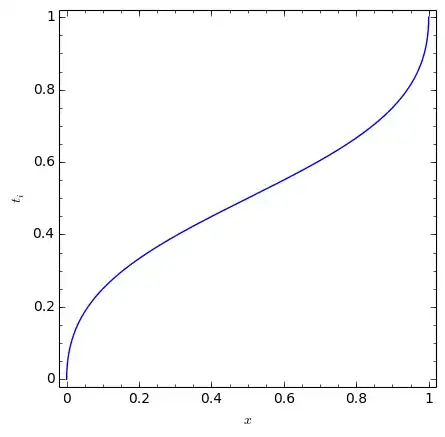
Solving this quadratic equation, you get two solutions, but the one which satisfies $0\le t\le 1$ is always the following, as can be seen from the plot below:
$$t_{\text{inflection}} = \frac{\sqrt{x-x^2} - x}{1 - 2x}$$
For $x=\frac12$ this expression is undefined, but you know that in that case the inflection point has to lie in the center, at $t=\frac12$.
If you don't have the coordinates above, you can define
$$ x := \frac{\lvert AB\rvert}{\lvert AB\rvert+\lvert CD\rvert} = \frac{B_x - A_x}{D_x - A_x} $$
and obtain $t$ using the same formula.
