Largest Equilateral Triangle in a Polygon

Question

Is there an algorithm to determine the largest equilateral triangle in a convex polygon?

Answer 1

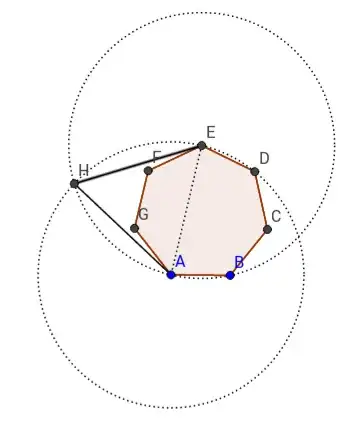
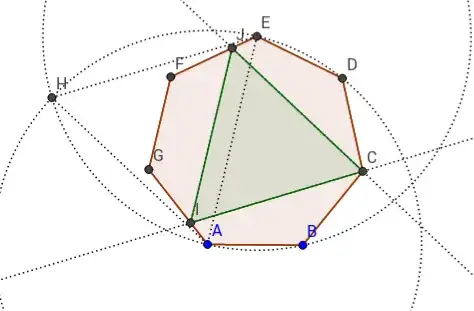
Based on my other answers to more specific tasks, I offer the following solution that will work for any regular convex polygon:

1. Draw the long diagonal AE, and draw circles at either end, with radius AE.

2. Mark H, the point of intersection of the two circles, and draw intervals HA and HE.

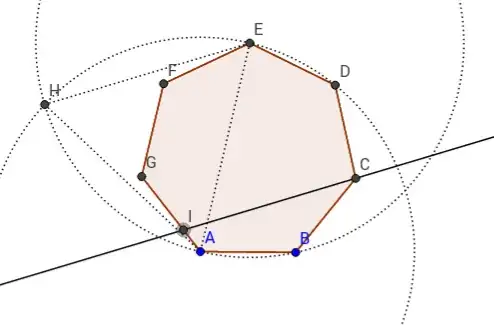
3. Draw a line parallel to HE through C, and mark I, the point of intersection with GA.

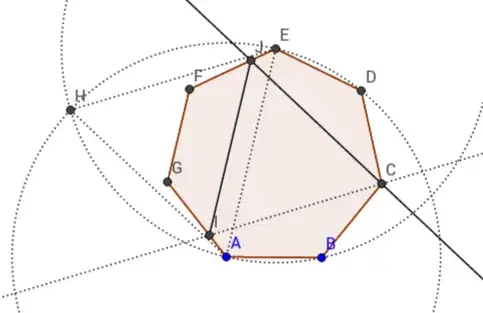
4. Draw a line parallel to HA through C, and mark J, the point of intersection with EF. Draw interval IJ.

5. Shade $\triangle$CEI, the required equilateral triangle.

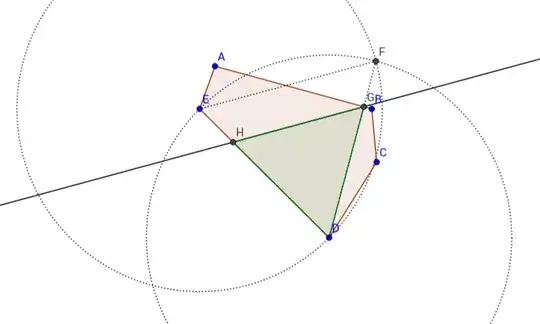
I submit the following example of the construction for an irregular polygon ...

and make the observations:

1. the inscribed equilateral triangle of maximum area within an irregular polygon will have one side on the polygon's longest side.

2. the inscribed equilateral triangle of maximum area within a regular polygon will have as it's axis of symmetry the longest axis of symmetry of the polygon.

Answer 2

My initial assumption is wrong, and an 80-80-20 triangle provides the coutnerexample.

---

If the triangle is maximal then all 3 vertices have to be on edges of the polygon. So I'm thinking that it makes sense to approach the problem by iterating over all tuples of 3 edges (filtering out tuples where all 3 edges are the same), assuming one vertex is somewhere on each of these edges, and seeking solutions using each tuple of edges.

Say $x_1$, $x_2$, and $x_3$, are the vertices of an equilateral triangle.

If $x_i$ is constrained to be on a line segment between $p_i$ and $q_i$, then $x_i = p_i \alpha_i + (1 - \alpha_i)q_i$ where $0 \le \alpha_i \le 1$ is an interpolation variable that puts each $x_i$ at a proportion of $\alpha_i$ along each line segment.

Define $v_1$, $v_2$, and $v_3$ as the vector edges of this triangle ($v_1 = x_1 - x_2$, $v_2 = x_2 - x_3$, $v_3 = x_3 - x_1$). We have $v_1 \cdot v_1 = v_2 \cdot v_2 = v_3 \cdot v_3$ since the lengths of the sides must be equal. Substitute the definitions of $v_i$ into these equations, then substitute the interpolation equations for $x_i$ above into that.

Now the equations look like $P_1(\alpha_1, \alpha_2, \alpha_3) = P_2(\alpha_1, \alpha_2, \alpha_3) = P_3(\alpha_1, \alpha_2, \alpha_3)$ where each $P_i$ is a 2nd degree multinomial. All solutions of these multinomials obeying the $\alpha$ range requirement form equilateral triangles touching the edge of the polygon.

Any particular instance of these equations could have 0, 1, or 2 solutions, maybe some other number, and possibly an infinite range of solutions (like a regular (or sufficiently symmetrical) polygon with 3n edges). If you find a finite number of solutions you can just test them to see which results in the largest edge size. If you find an infinite range of solutions then finding a maximal triangle is more complicated.

~~

Answer 3

Yes, there is an algorithm:

DePano, A., Yan Ke, and J. O’Rourke. "Finding largest inscribed equilateral triangles and squares." Proc. 25th Allerton Conf. Commun. Control Comput. 1987.

Unfortunately, I do not have easy access to my own article. :-/

---

      ^{(Image from this link.)}