Background: I asked this question on Stack Overflow about how to program in Java or VBA a method to calculate asymptotes given a range of data points. I believe the underlying question would be more appropriate here than on SO - if I understand the statistical way of solving the problem, I will be able to solve it programmatically.
Problem: We are given $n \in [5,15]$ numbers on the interval $]0,1]$ that are the measured approximations of some real-life phenomena, call them $s_1, s_2, \cdots, s_n$. They tend to be decreasing so that $s_i<s_{i+1}$ (although they are approximations so that it's not always so). Looking at them on a graph, we see that it appears they have a horizontal asymptote as $n \rightarrow \infty$. Example:
i value
- -
1 0.8232
2 0.6032
3 0.5012
4 0.4646
5 0.45001
6 0.44981
which gives the following chart
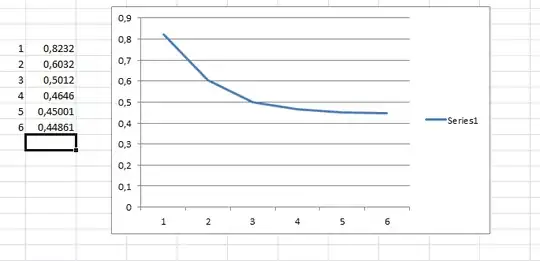
The horizontal asymptote would be $y=a$ with $a$ being some number less than $s_n$. In this case, it seems like $a$ is close to $0.44$. I have two questions:
How do we find this asymptote if we do not know the underlying distribution? (I guess we assume the formula $e^{ax}+b$, is this true?)
How do we find the asymptote for some confidence interval, say 95%? Do we then assume that the measurements are accurate or should we assume that each $s_i$ follows a normal distribution on its true value for some low standard deviation $\sigma_i$ (so that the chance that the true value corresponding to $s_i$ has a 67% change of being within $[s_i-\sigma_i,s_i+\sigma_i]$)?