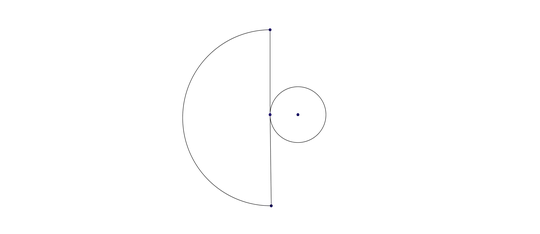
Coffeebelly was very close to the complete answer - you have to use a method similar to that one and integrate the polar area around the barn. Shamelessly stealing coffeebelly's picture:
https://i.sstatic.net/LYcMg.jpg
So - we know that the area to the left of the barn is easy - a semicircle with radius 16π, or A = 1/2 π(16π)^2 = 128π^3. Now for the hard part.
The area that the cow can graze around the barn is more complicated. The length of the rope shrinks as it goes around the barn. But we can integrate this area, using the regions shown in coffeebelly's picture. If we use an angle θ equal to the distance around the barn the cow's rope goes (where it departs the barn at a tangent), we get the following integral:
∫(from π to 0) (1/2 r^2 dθ), where r is the distance of rope left after departing the side of the barn, and dθ is the incremental angle.
Now, r = 16π - θ * (2πR / 2π radians) = 16π - θR = 16π - 16θ.
So the area to the right equals the integral:
A = ∫(from π to 0) (1/2 (16π - 16θ)^2 dθ) = 128 ∫(π to 0) (π - θ)^2 dθ
A = 128∫(π to 0) (θ^2 - 2πθ + π^2) dθ = 128 (1/3 θ^3 - π θ^2 + π^2 θ)|(π to 0)
A = 128(1/3 π^3 - π^3 + π^3) = 128/3 π^3
So the total area is (128 + 128/3) π^3 = 512/3 π^3.
Or exactly 2/3 the area of the entire circle.
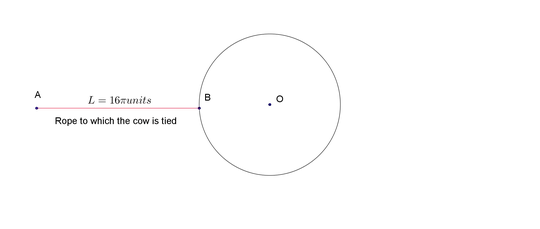
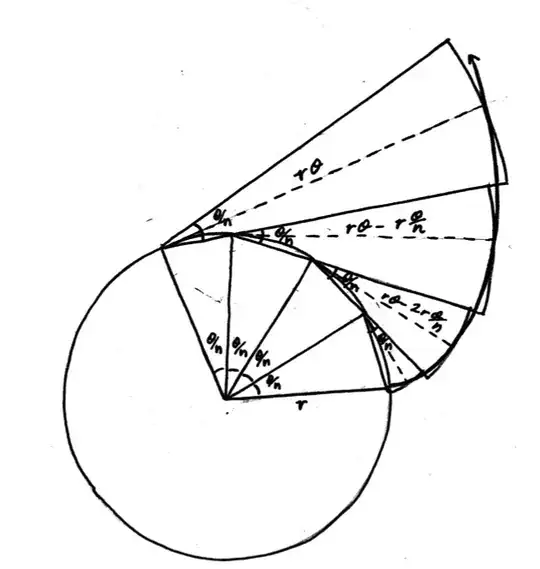 $n=4$ and $r$ is the radius of the barn. Taking the limit of the sum as $n\rightarrow\infty$ will get you the answer.
$n=4$ and $r$ is the radius of the barn. Taking the limit of the sum as $n\rightarrow\infty$ will get you the answer.