I follow the majority of this derivation I just do not understand where the two terms highlighted in green come from.
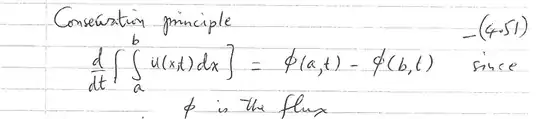

I follow the majority of this derivation I just do not understand where the two terms highlighted in green come from.
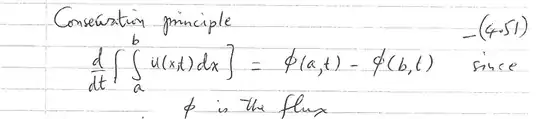

A hint that will help you think through this: A shock is like an "internal boundary". In particular, certain quantities (can you think which ones?) are discontinuous across shocks. If you think of the shock as an oriented curve, you must distinguish quantities on one side from those on the other side - that's what the (+) and (-) superscripts indicate.
Also, you might wish to look up Leibniz' rule of differentiation under the integral sign.
Ok, here's a more detailed answer. In the derivation, $s(t)$ is the instantaneous position of the shock, i.e. it is a function of time. As I mentioned earlier, some quantities are discontinuous across shocks. Now consider the first term in the conservation law:
$$ \frac{d}{dt} \int_{a}^{s(t)} u(x,t) dx $$
To compute this time derivative requires the use of Leibniz' rule of differentiation under the integral sign. Leibniz rule says that
$$ \frac{d}{dt} \int_{a(t)}^{b(t)} f(x,t) dx = \int_{a(t)}^{b(t)} \frac{\partial f(x,t)}{\partial t} dx + f(b(t),t) b'(t) - f(a(t),t) a'(t) $$ provided $\frac{\partial f(x,t)}{\partial t}$ exists and is continuous.
Returning to the original conservation law, you see that it is split in such a way (using the shock as a boundary), i.e., in fact
$$ \int_{a}^{b} u(x,t) dx = \lim_{\epsilon \rightarrow 0^+} \int_{a}^{s(t)-\epsilon} u(x,t) dx + \lim_{\epsilon \rightarrow 0^+} \int_{s(t)+\epsilon}^{b} u(x,t) dx $$
You have to remember that $u$ has a jump, i.e. it is different on either side of the shock. Let's return to the first term now; you want the derivative
$$ \frac{d}{dt} \lim_{\epsilon \rightarrow 0^+} \int_{a}^{s(t)-\epsilon} u(x,t) dx $$
Note that as long as $\epsilon > 0$, $u$ has continuous partial derivatives, i.e. you can apply the Leibniz rule to the integral for small positive epsilon. This gives
$$ \frac{d}{dt} \int_{a}^{s(t)-\epsilon} u(x,t) dx = \int_{a}^{s(t)-\epsilon} \frac{\partial u(x,t)}{\partial t} dx + u(s(t)-\epsilon, t) \frac{d(s(t)-\epsilon)}{dt} + 0 $$
The last term is 0 because your lower limit $a$ is not a function of time. It is customary to write $s(t)-\epsilon$ as $s^-$ for small epsilon. Also, $\epsilon$ is independent of t. So you finally have
$$ \frac{d}{dt} \int_{a}^{s^-} u(x,t) dx = \int_{a}^{s^-} \frac{\partial u(x,t)}{\partial t} dx + u(s^-, t) \frac{ds(t)}{dt} $$
You can carry out a similar procedure for the second term - there, the upper limit $b$ is independent of time and the lower is not. So on applying Leibniz rule you get
$$ \frac{d}{dt} \int_{s^+}^{b} u(x,t) dx = \int_{s^+}^{b} \frac{\partial u(x,t)}{\partial t} dx - u(s^+, t) \frac{ds(t)}{dt} $$
so now you see how the boxed terms enter the equation.