Solving for limit of integration

Question

$$\frac{1}{\sqrt{2\pi}} \int^0_{z_a} e^{\frac{-z^2}{2}} \, dz = 0.48 $$

How would I solve for the value of $z_a$ using a calculator?

Answer 1

Define

$$ f(z) = \frac{1}{\sqrt{2\pi}} \int_z^0 e^{-t^2/2}\,dt. $$

Here's a plot of $f(z)$:

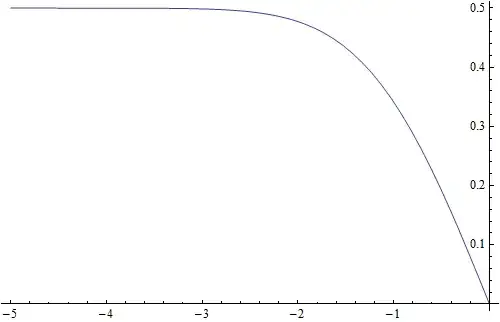
There are two notable features of this plot:

• When $z$ is close to zero, $f(z)$ is very close to $-\sqrt{2\pi} z$. Indeed, by calculating the derivatives using the fundamental theorem of calculus we can show that $$\begin{align} f(z) &= f(0) + f'(0)z + \frac{f''(0)}{2}z^2 + O(z^3) \\&= -\sqrt{2\pi}z + O(z^3) \end{align}$$ as $z \to 0$.

• When $z$ is away from zero, $f(z)$ is very close to $$\frac{1}{\sqrt{2\pi}}\int_{-\infty}^0 e^{-t^2/2}\,dt = \frac{1}{2}.$$

You're interested in solving the equation

$$ f(z) = 0.48, $$

and since $0.48$ is very close to $1/2$ we would expect that $z$ falls into the second category. Let's calculate an initial guess $z_0$ for $z$.

---

Splitting the integral then integrating by parts we get

$$ \begin{align} f(z) &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^0 e^{-t^2/2}\,dt - \frac{1}{\sqrt{2\pi}} \int_{-\infty}^z e^{-t^2/2}\,dt \\ &= \frac{1}{2} - \frac{1}{\sqrt{2\pi}} \int_{-\infty}^z e^{-t^2/2}\,dt \\ &= \frac{1}{2} + \frac{1}{\sqrt{2\pi}} \int_{-\infty}^z t^{-1} d\left(e^{-t^2/2}\right) \\ &= \frac{1}{2} + \frac{1}{\sqrt{2\pi}}\left(\left. t^{-1} e^{-t^2/2} \right|_{t=-\infty}^{t=z} + \int_{-\infty}^{z} t^{-2} e^{-t^2/2}\,dt\right) \\ &= \frac{1}{2} + \frac{1}{\sqrt{2\pi}} z^{-1} e^{-z^2/2} + \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} t^{-2} e^{-t^2/2}\,dt. \end{align} $$

This new integral with its factor of $t^{-2}$ in the integrand is surely much smaller than the original when $z$ is large and negative, so our first approximation to $f(z)$ in this case would be

$$ f(z) \approx \frac{1}{2} + \frac{1}{\sqrt{2\pi}} z^{-1} e^{-z^2/2}. $$

Here's a plot of $f(z)$ in blue versus this approximation in red:

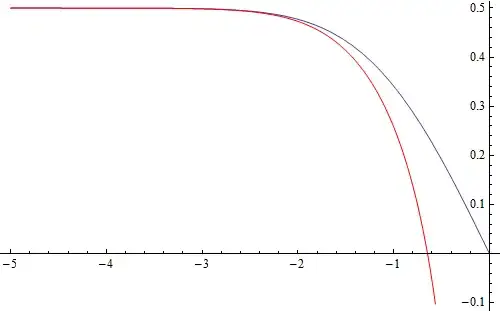
So, if we wanted to solve an equation like

$$ f(z) = \frac{1}{2}-\epsilon $$

(like we do, with $\epsilon = 0.02$), then we could get an approximate solution by instead solving

$$ \frac{1}{2} + \frac{1}{\sqrt{2\pi}} z^{-1} e^{-z^2/2} = \frac{1}{2}-\epsilon, $$

which is the same as

$$ -\frac{1}{\sqrt{2\pi} \epsilon} = z e^{z^2/2}. $$

Squaring this yields

$$ \frac{1}{2\pi \epsilon^2} = z^2 e^{z^2}, $$

which can be solved using the Lambert W function as

$$ z^2 = W(1/(2\pi \epsilon^2)). $$

Finally, taking the negative square root (remember we want $z$ to be negative) yields

$$ z = -\sqrt{W(1/(2\pi \epsilon^2))}. $$

For large $x$ it's known that $W(x) \approx \log x - \log\log x$ (for a proof see this answer), so for small $\epsilon$ we have

$$ z \approx -\sqrt{\log \frac{1}{2\pi \epsilon^2} - \log\log \frac{1}{2\pi \epsilon^2}}. $$

Thus our initial approximation $z_0$ for the solution to the equation

$$ f(z) = 0.48 = \frac{1}{2} - 0.02 = \frac{1}{2} - \epsilon $$

is

$$ z_0 = -\sqrt{\log \frac{1}{2\pi \epsilon^2} - \log\log \frac{1}{2\pi \epsilon^2}}{\Bigg |}_{\epsilon = 0.02} \doteq -2.04859. $$

---

Now, using this initial guess $z_0 = -2.04859$, we can obtain a more precise value for the root of

$$ f(z) = 0.48 $$

by using Newton's method. Let's define $g(z) := f(z) - 0.48$, so that the equation we want to solve is

$$ g(z) = 0. $$

Using the fundamental theorem of calculus we can calculate

$$ g'(z) = - \frac{1}{\sqrt{2\pi}} e^{-z^2/2}, $$

so the iteration for Newton's method,

$$ z_{n+1} = z_n - \frac{g(z_n)}{g'(z_n)}, $$

is

$$ z_{n+1} = z_n + e^{z_n^2/2} \left(\int_{z_n}^0 e^{-t^2/2}\,dt - 0.48\sqrt{2\pi}\right). $$

We then iterate this recurrence using the starting value $z_0 = -2.04859$ to obtain better approximations for the root. Mathematica produces the iterates

$$ \begin{align} z_1 &= -2.05372, \\ z_2 &= -2.05375, \\ z_3 &= -2.05375, \end{align} $$

so it looks like the root is $z \doteq -2.05375$ to six significant figures. Indeed, the root is approximately

$$ z \doteq -2.05374\ 89106\ 31823\ 05294. $$

The Casio fx-991EX PLUS has a button for numerical integration so this iteration process should be doable on your hand calculator.