Newly Developed With Details - Describing orthographic projection using simple 2D transformations

Question

Thanks to Pedro for helping me further develop my question into something tangible. His (most recent) answer below clearly and formally outlines what I am asking.

---

This is similar to this question, except in 3D and involving surfaces.

I am doing some graphics work involving rotation matrices. The problem is that I am not just transforming points, I'm also transforming arbitrary surfaces (images, colors, etc.)

These surfaces are represented by rectangles and only really support two main transformations, rotation and scaling (along the horizontal and vertical axes).

If I have a rotation matrix: $$ M = \left(\begin{matrix} m_0 & m_1 & m_2 \\ m_3 & m_4 & m_5 \\ m_6 & m_7 & m_8 \\ \end{matrix}\right) $$

That might produce some rotation like this: (just for illustration purposes)

It could be said that in order to achieve this shape, a rectangle would go through a certain counter-clockwise rotation and then a certain scaling along the horizontal axis and the vertical axis. Is there any way to figure out what that counter-clockwise angle is and what the scale factors are? Keep in mind that I said that the rotation occurs first, though this is arbitrary and the rotation and scale transformations could happen in any order.

EDIT: Hopefully these details grant more clarity.

Here's exactly what's happening.

1. There is a set of points (a, b, 0) that represent 3D coordinates. Each of these points have a related surface represented by a width and height. That surface could be an image, a color or any other shape potentially. These surfaces support two main transformations: rotation and scale transformations. The scale transformations occur in the horizontal and vertical axis and the rotations occur around an axis perpendicular to the screen.
2. Assume the plane of the screen is the reference point from which all rotations occur. Also assume that there is a matrix M as defined above that represents the orientation of the 3D coordinate plane on which (a, b, 0) resides.
3. What I am trying to do is project the point (a, b, 0) AND its related surface onto the screen using the aforementioned matrix. Taking that point (a, b, 0), as well as an orientation matrix in as input, I would like to figure out how I should transform the surface so that it appears as it would in 3D on the 2D screen (i.e. how I can transform it so that it looks projected on the screen). The image above is a good example of a surface that while looking 3D, is actually somehow represented by a set of 2D points. I would like to know how to come up with that projection given that I do not have the full point array.

My assumption, which I now see may be incorrect, was that you could do that with a rotation and a scale alone. An answer below demonstrated that in fact you need at least another angle called the shear angle.

Another piece of information that may be useful: As I mentioned, this is graphics work, so the coordinate axis are actually flipped. The x-axis is the same, but the y-axis is flipped so it becomes more positive as you go down.

Hopefully making my question a bit more broad will lead to an answer: What transformations do I need to project a flat 3D surface onto a 2D plane (the screen)?

Answer 1

After further clarifications in chat, it's now clear what the OP wanted, and my other solution did not apply at all.

It's an interesting problem. I didn't find an optimal solution but I found a solution. Anyone's welcome to provide a better one.

The problem

The OP has a 3D rotation matrix $M$ and a figure of arbitrary size on the plane of the screen that he wants to transform by $M$.

His desired visual result is the 3D rotation of the figure by the matrix $M$, followed by an orthographic projection on the screen plane obtained by discarding the $z$ component.

However, he can't just perform that operation, and instead the only operations over the figure he can do are scaling horizontally/vertically and rotating, all in 2D.

His goal, thus, is to find out which of these 2D transforms to apply, and in which order, for obtaining the same visual result as if the figure was transformed by the matrix $M$ and then projected orthographically on the screen by discarding the $z$ component.

Reduction

First, note that applying the rotation matrix, $M=\pmatrix{m_0&m_1&m_2\\m_3&m_4&m_5\\m_6&m_7&m_8}$, to the figure to represent and then projecting it orthogonally by discarding the $z$ component, has the same effect as applying the 2D transform $\pmatrix{m_0&m_1\\m_3&m_4}$ to the figure. This is easy to show: taking the screen as a plane in 3D and its origin as the reference coordinate system, the vectors of the untransformed basis are $(1,0,0), (0,1,0), (0,0,1)$, and therefore the vectors of the transformed basis are $(m_0,m_3,m_6), (m_1,m_4,m_7), (m_2,m_5,m_8)$. Nothing lies outside the z=0 plane so we don't need $(m_2,m_5,m_8)$ at all. After projecting the basis orthogonally by removing the $z$ component, we get a new 2D basis $(m_0,m_3), (m_1,m_4)$, which is the matrix.

Now the problem is reduced to the following, interesting question:

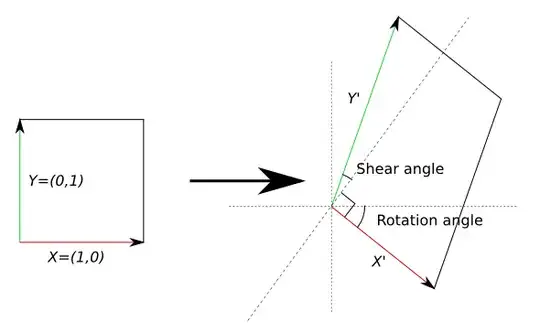
Given an arbitrary linear 2D transform matrix $\pmatrix{m_0&m_1\\m_3&m_4}$ (which may include shear), how can it be decomposed into a product of horizontal&vertical scaling matrices, and rotation matrices?

Optimal solution

It's clear that there are many possible solutions. However, I don't see how it can be done generally in less than the following three steps:

1. Rotate it by the angle $\theta$ necessary for the next scaling step to get the correct dimensions and shear.
2. Perform the scaling that will give it the correct shape.
3. Rotate it by another angle $\phi$ to get the correct orientation.

In other words, find parameters $\theta, s_x, s_y, \phi$ such that:

$$\pmatrix{\cos\phi&-\sin\phi\\\sin\phi&\cos\phi} \pmatrix{s_x&0\\0&s_y} \pmatrix{\cos\theta&-\sin\theta\\\sin\theta&\cos\theta} = \pmatrix{m0&m1\\m3&m4}$$

The trickiest part by far is to find the angle for (1), as (2) and (3) would be relatively easy (or vice versa: to find the angle for (3) and then (2) and (1) would be easier). I couldn't figure it out: when I attempted it, I got a big system of nonlinear equations that represent the constraints, bigger than I could cope with.

My solution

I've found a four-step solution (five in some cases, see edit). It works backwards from the rhomboid, as follows:

1. Scale the rhomboid horizontally until all sides are equal. We get a rhombus. If the shape was flipped, we make the scale negative. Alternatively, if negative scale is not applicable, or flipped surfaces are not desirable, don't paint the surface at all and stop here if it's flipped. (Flipping is handled in a separate step. See code.)
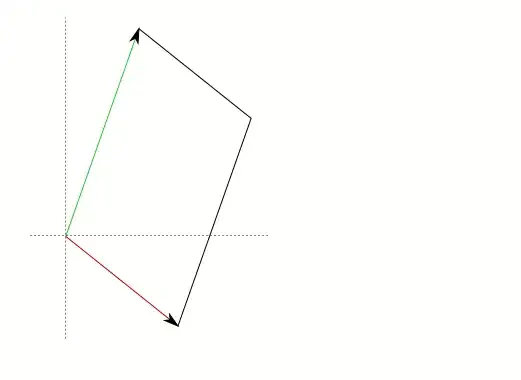
2. Rotate the rhombus so the diagonal that starts at the origin is horizontal.
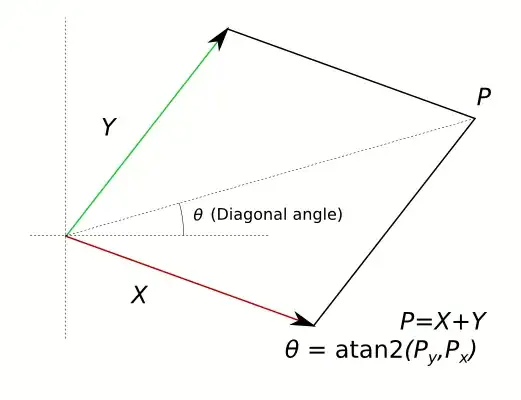
3. Scale the rhombus horizontally and vertically to get a unit square.
4. Rotate the square to make it upright and get the original $\pmatrix{1&0\\0&1}$ basis.

Once we have the steps, applying them in reverse order will perform the desired transform.

Step 1 works as follows. We have $(m_0,m_3), (m_1,m_4)$, the basis of the target transform. We want to find a scale factor $k$ such that $(m_0k)^2+m_3^2=(m_1k)^2+m_4^2$, i.e. such that when scaling the $x$ components by $k$, the lengths of the transformed basis vectors are equal. Solving for $k$ we get: $k=\sqrt{\frac{m_4^2-m_3^2}{m_0^2-m_1^2}}$, but we apply the sign of the determinant of the matrix $m_0m_4-m_1m_3$ to it, to unflip it if it was flipped.

For step 2, the angle of the transform is simply minus the angle of the diagonal: $\theta=-\mathrm{atan2}(m_3+m_4, (m_0+m_1)k)$

For step 3, we need to scale both diagonals so that their final length is $\sqrt 2$ (the diagonal of a unit square). Since in step 2 we just rotated, for this step we can take the diagonal of the vectors before being rotated, as their lengths will be the same. These diagonals are $\|((m_0+m_1)k, m_3+m_4)\|$ and $\|((m_0-m_1)k, m_3-m_4)\|$, therefore dividing $\sqrt 2$ by them will give us the scale factor in each axis.

Lastly, step 4 is simply a 45° rotation.

But you need to apply these steps in reverse to get the desired result. First, calculate $j=1/k=\sqrt{\frac{m_0^2-m_1^2}{m_4^2-m_3^2}}$, then:

1. Rotate by -45°.
2. Scale by $$s_x=\frac{\|(\frac{m_0+m_1}{j}, m_3+m_4)\|}{\sqrt 2},\,\,s_y=\frac{\|(\frac{m_0-m_1}{j}, m_3-m_4)\|}{\sqrt 2}$$
3. Rotate by $\theta=\mathrm{atan2}(m_3+m_4, (m_0+m_1)/j)$
4. Scale horizontally by $\mathrm{copysign}(j, m_0m_4-m_1m_3)$

That should give the desired result. Note the caveat that if $|m_4|=|m_3|$, then you would get a division by zero when calculating $j$, and if $|m_0|=|m_1|$, you would get it when dividing by $j$. The interpretation of that and the action to take if that case arises, is left as an exercise to the reader

EDIT: OK, that was lazy, so let me expand. If both absolute value equalities match, it's telling us that either the vectors match, or they are aligned and opposite, or we already have a rhombus and are ready to get a square by just scaling (but it has to be considered which of four possible angles the diagonal is at, and act accordingly, considering flipping too) (flipping is done as a separate step). However, there's yet another case that I hadn't considered: when calculating $k$, we might be trying to take the square root of a negative number. If that's the case, then the problem is that there's no possible scale value that allows transforming the rhomboid into a rhombus. In that case, starting by a rotation of the initial rhomboid to bring the diagonal longest vector to the X axis (that is, a rotation by $\phi=-\mathrm{atan2}(m_3,m_0)$ or $\phi=-\mathrm{atan2}(m_4,m_1)$, whichever is the longest) should suffice to make $k$ valid. In that case, don't forget to apply that rotation as the last step when doing it forwards. That will help also in the case that the denominator of $j$ is zero or $j$ itself is zero.

Note: It's possible that the angles should be applied with the sign changed, given that the sign of the Y axis is reversed.

EDIT 2: Proof of concept using the pygame API:

import pygame, math

# Includes the minus sign necessary for rotating in the right direction
RAD_TO_DEG = -180/math.pi

def Transform3D(Surf, M):
    """Transform a surface by an arbitrary 2D or 3D matrix.

    Returns the transformed surface or None if it's not visible.
    """
    tol = 0.0001 # tolerance for too low scale

    # Aliases for commodity
    flip = pygame.transform.flip
    rotate = pygame.transform.rotate
    scale = pygame.transform.smoothscale # or .scale, your choice

    m0 = M[0][0]
    m1 = M[0][1]
    m3 = M[1][0]
    m4 = M[1][1]

    # Determinant zero?
    det = m0*m4 - m1*m3
    if abs(det) < tol:
        # Aligned - don't draw
        return None

    # Determinant negative?
    if det < 0:
        # Toggle the basis vectors
        m0,m1 = m1,m0
        m3,m4 = m4,m3
        # Flip and rotate to act as if X and Y were inverted
        Surf = rotate(flip(Surf, True, False), 90)

    # Calculate the numerator and denominator of k
    kn = m4*m4 - m3*m3
    kd = m0*m0 - m1*m1

    Phi = 0 # Fixup angle to allow getting a rhombus by horizontal scaling

    if abs(kd) < tol and abs(kn) < tol:
         # We have either a rhombus or aligned vectors. Which is it?
         # We test that by checking if there's exactly one different sign
         # (by checking the parity)
         if (m0 < 0) ^ (m1 < 0) ^ (m3 < 0) ^ (m4 < 0):
             k = 1

         else:
             # Quadrants are opposite or equal - vectors are same length and
             # either matching or opposite
             return None # Don't paint
    else:
        # Rhomboid.

        # There's work to do. First, check if we can get a rhombus by
        # scaling horizontally.
        if ((kn < 0) ^ (kd < 0)) or abs(kn) < tol or abs(kd) < tol:
            # This would generate a negative square root, or a zero or
            # infinite k, meaning that scaling horizontally to get a rhombus
            # is not possible. Deal with it by applying a rotation as an extra
            # last step, and transforming the input matrix.

            # Rotate to bring the largest side to the X axis
            if m3*m3 + m0*m0 > m4*m4 + m1*m1:
                Phi = -math.atan2(m3, m0)
            else:
                Phi = -math.atan2(m4, m1)
            c = math.cos(Phi)
            s = math.sin(Phi)

            # Apply the rotation to our matrix

            m0,m1,m3,m4 = c*m0-s*m3, c*m1-s*m4, s*m0+c*m3, s*m1+c*m4

            # Recalculate the numerator and denominator of k
            kn = m4*m4 - m3*m3
            kd = m0*m0 - m1*m1

            # Signs should be equal now
            assert (kn >= 0) ^ (kd < 0)

        k = math.sqrt(kn / kd)

    # All angles are inverted in the calls to rotate()

    # First rotate the surface by -45 deg
    Surf = rotate(Surf, 45)

    # Scale it appropriately
    sx = ((m0+m1)*k)**2+(m3+m4)**2
    sx = int(math.sqrt(sx*0.5) * Surf.get_width() + 0.5)
    sy = ((m0-m1)*k)**2+(m3-m4)**2
    sy = int(math.sqrt(sy*0.5) * Surf.get_height() + 0.5)
    Surf = scale(Surf, (max(sx, 1), max(sy, 1)))

    # Rotate by the required angle
    Surf = rotate(Surf, math.atan2(m3+m4, (m0+m1)*k)*RAD_TO_DEG)

    # Scale horizontally to get the correct shape
    sx = int(Surf.get_width()/k+0.5)
    Surf = scale(Surf, (max(sx, 1), Surf.get_height()))

    if Phi:
        # Apply the final rotation if necessary
        Surf = rotate(Surf, -Phi*RAD_TO_DEG)

    # Get our prize
    return Surf


import time

def main(M):

    width, height = 320, 240
    screen = pygame.display.set_mode((width, height))

    fig = pygame.image.load("square.png")
    origfigrect = fig.get_rect()

    black = (0, 0, 0)

    surf = Transform3D(fig, M)
    if surf is None:
        fig.fill(black)
    else:
        fig = surf

    Axes = False # toggles every .4 seconds to blink the axes

    while 1:
        for event in pygame.event.get():
            if event.type == pygame.QUIT: return

        screen.fill(black)
        figpos = (160-fig.get_width()/2, 120-fig.get_height()/2)
        screen.blit(fig, figpos)
        Axes = not Axes
        if Axes:
            Cx = (M[0][0]+M[0][1])*0.5 * origfigrect.w
            Cy = (M[1][0]+M[1][1])*0.5 * origfigrect.h
            Ox = int(width/2 - Cx + 0.5)
            Oy = int(height/2 - Cy + 0.5)
            L1x = int(M[0][0]*origfigrect.w + Ox + 0.5)
            L1y = int(M[1][0]*origfigrect.h + Oy + 0.5)
            L2x = int(M[0][1]*origfigrect.w + Ox + 0.5)
            L2y = int(M[1][1]*origfigrect.h + Oy + 0.5)
            pygame.draw.line(screen, (0,255,0), (Ox, Oy), (L2x, L2y))
            pygame.draw.line(screen, (255,0,0), (Ox, Oy), (L1x, L1y))
        pygame.display.flip()
        time.sleep(.4)


pygame.init()
main([[0.473021, 0.579769, 0.663414],
      [-0.296198, 0.813798, -0.500000],
      [-0.829769, 0.040009, 0.556670]]
    )
pygame.quit()

Sample image used for my tests:

(Note that while adding the code, I've hit a bug in SE where the 0's and 1's within square brackets in the code were replaced by other numbers - I hope I've caught and restored all of them correctly.)

Edit 3: I asked the specific question about the decomposition, and got an answer which finds the optimal solution: Decompose a 2D arbitrary transform into only scaling and rotation

Answer 2

It's not clear from your question, but it seems to me that given an arbitrary linear transformation matrix, you need at least to specify a shear angle as well. Consider a matrix that transforms a rectangle into this figure:

That transform is not the result of one single rotation followed by one single scaling on each axis, nor vice versa.

The best approach might be to derive X scale, Y scale, rotation angle and shear angle (with X and Y scale applied before rotation). Here's how:

• Transform the vectors $X=(1,0)$ and $Y=(0,1)$ by the matrix, obtaining $X'$ and $Y'$.
• $||X'||$ (the length of $X'$) is the X scale factor.
• $||Y'||$ (the length of $Y'$) is the Y scale factor.
• $\theta_X = \mathrm{atan2}(X'_y, X'_x)$ is the rotation angle.
• Obtain $\theta_Y = \mathrm{atan2}(Y'_y, Y'_x)$ (the angle of the transformed Y vector).
• $(\theta_Y-\theta_X-90°) \bmod (360°)$ is the shear angle.

This diagram will hopefully help understanding the shear and the reasoning: