Understanding matrices.

Question

I'm trying to understand matrices.

As far as I can understand, a matrix is a way to represent data (?) or some sort of function on data (?).

However apart from the fact that they're a way to represent data (?), I really don't understand why we need them and what they're for. I'll give you an example:

I'm a game developer, and in my games I often use the well known rotation matrix. When I want to rotate a shape by some angle, I do this for every vertex:

newX = cos(angle) - sin(angle)
newY = sin(angle) + cos(angle)

This works great.

However, I don't understand why we need to represent it as a matrix (a table). The formula written above works great, what do I gain by thinking of it as a matrix?

Please explain to me what I gain by using matrices (tables) and what exactly they're used for. And please go easy on the math.

Answer 1

Suppose you're working on a car racing game. You want to render, in 3D, a feature on a spinning wheel of a car that is itself spinning. The location of the feature is given by a translation from the centre of the wheel, followed by a rotation of the wheel, followed by a translation from some point of reference on the car, followed by the rotation of the car which is itself translated. That's 4 or 5 transforms in a row, depending on how you look at it. You don't want to perform 5 transforms for every feature on the wheel.

If you have a linear map on an $n$-dimensional space then once you've sampled the value of the map at $n$ points (that form a basis) you can deduce what the value is at any point in the space. So if you want to evaluate a linear mapping at 100 points in a 3D space, you only have to evaluate it at 3 points and you can use the result to compute the value at all 100 points. This is true even if the linear mapping is a composition of a billion transforms. You can perform the billion operations on just 3 points and then extending to 100 points is a trivial extra bit of work. And that's the point of matrices: it gives a way to organise your computations so that you only have to apply your sequence of transforms to a handful of points. That process gives you a single transform that summarises the combination of all of the transforms, and then applying that to the rest of the points is a simple computation.

In the case of the spinning wheel: you only have to perform your 4 or 5 transforms for just 4 points and that will give you a matrix. You can now use this matrix to quickly compute the transform for every other point on the wheel. You don't have to separately compute the sequence of 4 or 5 operations for every single point.

Addendum: if you're wondering why 4 points are required, not just 3, see my answer here: Why are $3D$ transformation matrices $4 \times 4$ instead of $3 \times 3$?

Answer 2

As you point out, matrices are simply a way of writing down certain kinds of functions. Here you're dealing with the function that sends a point $(x, y)$ to its image under a rotation. Since the new coordinates are simply the old ones, multiplied by coefficients and added together, we can specify the function just by specifying the coefficients. A table is a then a convenient way to write them down.

There's really not much more to it, it's just a convenient shorthand.

You might understand it better by noting that it's not like this is just something we do for rotations. We do it for any linear function, which is a function in which we map several input values to several output values by multiplying the inputs by certain coefficients and adding them together. Again, any such function can be determined just by knowing the coefficients, so a shorthand form for writing the function down is to just write the coefficients in a table. That is, let's say we have a function given by:

$$\begin{align} \text{newX} = a\cdot\text{oldX} + b\cdot\text{oldY} \\ \text{newY} = c\cdot\text{oldX} + d\cdot\text{oldY} \end{align}$$

The only information we need to specify this function is the numbers $a, b, c$ and $d$, so we can represent this function with the matrix $\bigl(\begin{smallmatrix}a&b\\ c&d\end{smallmatrix} \bigr)$. And similarly for more than $2$ inputs/outputs.

The question is: why are linear functions important enough to deserve a special shorthand notation? It's because of where they fit this Venn diagram:

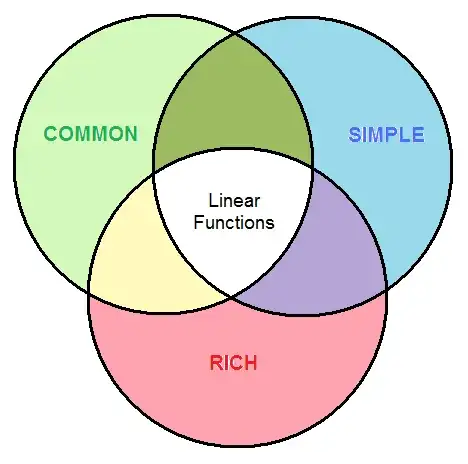
Linear functions are common, they occur frequently in applications, which isn't too surprising, given that "multiply by coefficients and then add" is a pretty simple type of rule. They are simple, it's very easy to calculate with them and solve problems involving them. And they are mathematically rich, there's a lot to say about them, many interesting mathematical phenomena emerge from linear functions.

Now, if you're using a graphics framework such as Flash with ActionScript 3, it may require you to rotate graphical objects using code something like this:

rotate = new Matrix(cos, -sin, sin, cos);
sprite.applyMatrix(rotate);

And perhaps you're wondering why it's not just:

sprite.rotate(angle);

(Of course, a lot of frameworks do have functions like the second one, but I suspect that under the hood they're still doing something like the first example).

I suppose this is just to allow you to apply arbitrary linear functions to your sprite, rather than just rotations (such as scalings, skewings, and flips), while maintaining a simple back-end in the graphics engine. This way, if you apply several linear transformations at once, since you're supplying them as matrices, the program can simply combine the matrices into one, and apply all the linear transformations at the same time, which is presumably computationally less expensive.

Answer 3

Matrices are ubiquitous in computer graphics (such as games) because they are very powerful:

(1) They can represent many different kinds of transformations in a uniform way, including:

• Rotation
• Translation
• Scaling
• Shearing
• Mirroring
• Orthographic projection
• Perspective projection
• Any combination of these

This simplifies code design and offers great flexibility. For example, in a scene graph we may allow assigning a 4x4 transformation matrix to a node and we can immediately use all these transformations.

(2) Chains of transformations can be merged into a single matrix by multiplying the corresponding matrices. This is a big deal for rendering performance!

A scene consists of many thousands or even hundreds of thousands of vertices. Each of them needs to be transformed from the model space to world space to view space to screen space. We can precalculate this transformation (ModelViewProjection matrix) and save a lot of computations.

(3) We sometimes need to reverse a transformation, e.g. to find out which object has been clicked by the user. With matrices, this is easy: Just calculate the inverse.

Answer 4

One benefit that hasn't been explicitly mentioned in the other answers so far is that matrices can be composed. Suppose you have transformations $T_1$ and $T_2$ that you want to apply to a lot of points. If these transformations are not implemented as matrices, you'd just have to literally apply $T_1$ and then $T_2$ to all the points. However, if the transformations are represented as matrices, you can compute a single matrix $T_3$ that corresponds to "do $T_1$ and then $T_2$" and apply that single matrix to all the points. Since $T_3$ is very easy to compute, that means you've cut your work in half.

Suppose that $T_1 = \begin{pmatrix}a&b\\c&d\end{pmatrix}$ and $T_2 = \begin{pmatrix}e&f\\g&h\end{pmatrix}$. The result of applying $T_1$ to $\begin{pmatrix}x\\y\end{pmatrix}$ is

$$\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}ax+by\\cx+dy\end{pmatrix}\,;$$

applying $T_2$ to that gives

$$\begin{pmatrix}e&f\\g&h\end{pmatrix}\begin{pmatrix}ax+by\\cx+dy\end{pmatrix} = \begin{pmatrix}e(ax+by)+f(cx+dy)\\g(ax+by)+h(cx+dy)\end{pmatrix} = \begin{pmatrix}(ae+cf)x + (be+df)y\\(ag+ch)x + (bg+dh)y\end{pmatrix}\,.$$

But this is exactly the same as $$\begin{pmatrix}ae+cf & be+df\\ ag+ch & bg+dh\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}\,,$$ so you can call this new matrix $T_3$, compute it once (now you can see how cheap it is) and then apply it to all your points. We write $T_3=T_2T_1$; note that this isn't necessarily the same as $T_1T_2$, which would mean "Do $T_2$ and then $T_1$." The same principles apply to higher-dimensional matrices.

Answer 5

Matrices appear first in history as a way to represent the coefficients of a linear system in a strcuture that has rows and columns. Suppose you have the linear system of equations: $$ax + by = e\\cx + dy = f$$ You can solve this system by doing row addition, subtraction, and multiplication by scalar.

It is boring to rewrite the entire system after you do some row operation, so we can write only the coefficients of $x$ and $y$ in a structure that we will call matrix: $$\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} e \\ f \end{bmatrix}$$ We can, then, add, subtract, and multiply the rows of this matrix $\begin{bmatrix} a & b \\ c & d \end{bmatrix}$ without worrying about the coefficients.

When you do these operations in a way that you eliminate $y$ , you will find that: $$x = \frac{ed-bf}{ad-bc}$$ And when you do the same for $x$ you will find: $$y = \frac{af-ec}{ad-bc}$$ You will always find a solution for the system, when $ad-bc\neq0$, so let's call this number $ad-bc$ as 'determinant', because it will determinate when the system has a solution.

This rule works for any square system of equations, not only the 2x2 case, but then the determinant will be different. The generalization of this is called Cramer's rule

If we progress in our study of matrices, we can then define transformations, that are ways to multiply a matrix by a vector, (in your case, a vector is a single column matrix that has the components $x$ and $y$, and they specify the position of your object. A vector is just a point $(x,y)$ in your game) this will transform the vector (for example: rotate, scale and translate it). When we generalize it, we can then multiply a matrix that rotates a vector, by a matrix that translates it, and then multiply by a matrix that scales it, and get a single matrix that, when multiplied together with the vector, will do these 3 transformations at the same time. This has a great utility in computer graphics.

The formula you use in your games is a way to apply a rotation in a vector $\begin{bmatrix} x \\ y \end{bmatrix}$, like this:

$$\begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta \\\end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \mbox{newX} \\ \mbox{newY} \end{bmatrix}$$

If you multiply this matrix with the vector $(x,y)$ you will obtain the 'formula' you have in your question.

While you're only working with a simple rotation, you can generalize matrices do to everything you want, and to create your own matrices, that will do a particular transformation you need. That way, you can use your graphic card to multiply these matrices faster than your computer would do, and get better results.

If you want to discover how to crate this rotation matrix, and other types of matrix, you can watch the Khan Academy series of videos in linear transformations, it will explain how to find this formula for the 2D and 3D cases, and also how to multiply different transformation matrices together.